Résolution du Unicorn (méthode des centres)
06
Oct
2022
Par morphocode
L' Unicorn est un cube merveilleux et passionnant, j'avoue que j'ai du mal à m'en sortir!,
J'ai mis plusieurs jours pour trouver un algorithme de résolution, la résolution se fait par plusieurs phases, accrochez-vous !!!!!
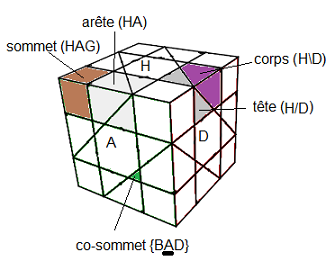
Notation
Pour nous les faces et les couleurs sont ainsi:
H(aut)=b(lanc) , B(as)=j(aune) , A(vant)=v(ert) , P(ostérieure)=k(lein) , G(auche)=o(range) , D(roite)=r(ouge)
Les rotations Rubik
A = tourner 90° la face Avant dans le sens horaire.
A' = tourner -90° (dans le sens antihoraire)
A² = tourner 180°
Les rotations Dino
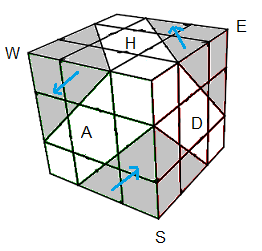
W=(HAG), E=(HPD), N=(BPG), S=(BAD).
W = tourner 120° le sommet (HAG) dans le sens horaire.
W' = tourner -120° (dans le sens antihoraire)
 |
 |
| Notation |
Rotations Dino |
1- Rendre les 4 rotations Dino disponibles
-On vérifie si les centres sont corrects (co-sommet pointe vers le sommet Dino)
-Puis on oriente les arêtes
Pour ça on se fait aider par plusieurs formules:
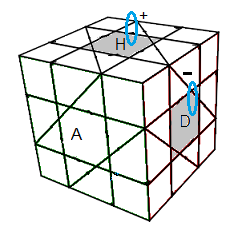
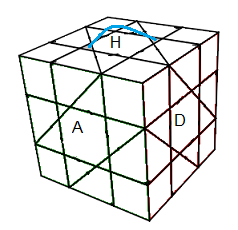
¤ Pivoter 2 centres : (H)
+(D)
- = ]Hd]]H'd] = Hdh'd' .H'dhd'
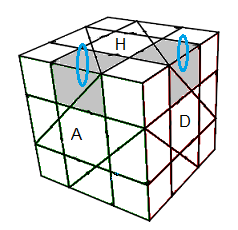
¤ Pivoter 2 arêtes : (HA)°(HD)° = [AD'][H'D]
 |
 |
| (H)+(D)- = ]Hd]]H'd] = Hdh'd' .H'dhd' |
(HA)°(HD)° = [AD'][H'D] |
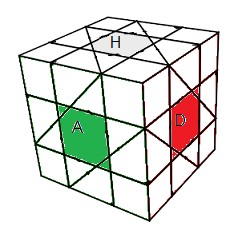
2- Finir les centres carrés
Avec les rotations Dino W,E,N,S et les rotations Rubik-carrés ,H²,B²,D²,... on peut facilement former les centres, c'est facile et intuitif .
 |
|
| Ce qu'on veut |
|
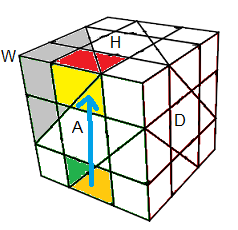
3- Former les arêtes
NOTE:
A. On essaie d'avoir toujours 3 mauvaises arêtes sur le tétraèdre "W"
B. Les rotations Rubik détruisent les rotations Dino, mais ce n'est pas grave car il suffit de garder un seul tétraèdre
 |
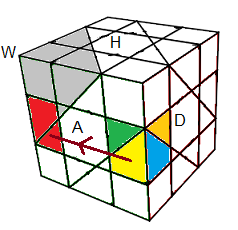 |
| (BA)->(HA) = B'A²BA² |
(AD)->(AG) = DA²D'A² |
 |
|
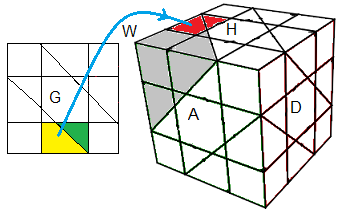
| (BG)->(HG) = B'G²BG² |
|
C'est assez long, la technique est comme on forme les arêtes dans le Revenge (4x4x4).
ça se fait en deux étapes
1) On forme d'abord l'arête
2) Ensuite on remplace la bonne arête par une mauvaise arête
3a. Former une arête
* On regarde le corps en (HG)
* Puis on cherche la tête et on la place en (HA)
(BA)->(HA) = B'A²BA² ; (BA) orientation opposée à (HA)
(BA)° = A'D'AB'D
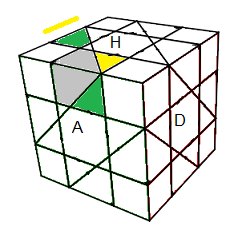 |
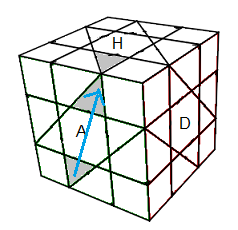 |
| Ce qu'on veut: corps en (HG), tête en (HA) |
(BA)->(HA) = B'A²BA² ; (BA) orientation opposée à (HA) |
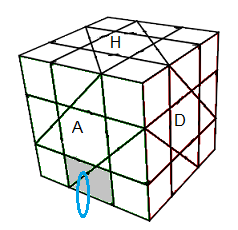 |
|
| (BA)° = A'D'AB'D |
|
3b. Remplacer une bonne arête contre une mauvaise arête
* Bonne arête en position: corps en (HG), tête en (HA)
* Mauvaise arête en (BA) avec l'orientation opposée à (HA)
(BA)->(HA) = WB'A²BA²W'
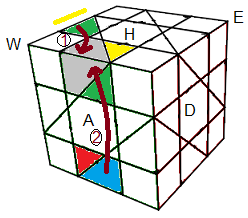 |
|
| (BA)->(HA) = WB'A²BA²W' |
|
3c. Cas particulier :
¤ 3 mauvaises arêtes en position "+" (sens horaire ==> bonnes arêtes)
Principe:
* On remplace la mauvaise arête en (AG) par une bonne arête en (AD) ; sens opposée
* On remplace la bonne arête en (HA) par la mauvaise arête en (BD)
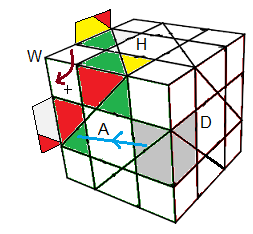
(HG)->(HA)->(AG) = [DA²] .W[A²B']W' = DA²D'A² .WA²B'A²BW';bonne arête en (AD) opposée à (AG)
 |
|
(HG)->(HA)->(AG) = [DA²] .W[A²B']W' = DA²D'A² .WA²B'A²BW'
bonne arête en (AD) opposée à (AG) |
|
¤ 3 mauvaises arêtes en position "-" (sens antihoraire ==> bonnes arêtes)
Principe:
* On remplace la mauvaise arête en (HA) par une bonne arête en (BA) ;sens oppoée
* On remplace la bonne arête en (AG) par la mauvaise arête en (BD)
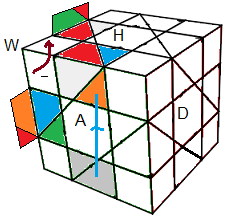
(HG)->(AD)->(HA) = [B'A²] .W'[A²D]W = B'A²BA² .W'A²DA²D'W ;bonne arête en (BA) opposée à (HA)
|
 |
| |
(HG)->(AD)->(HA) = [B'A²] .W'[A²D]W = B'A²BA² .W'A²DA²D'W
bonne arête en (BA) opposée à (HA) |
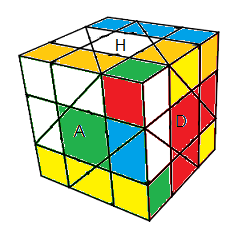
4- Résoudre comme un Rubik's Cube
Ici on a un Rubik's Cube on résout normalement
.::ICI::.
Si les centres ne sont pas bien orientés, on les oriente :
(H)
+(D)
- = ]Hd]]H'd] = Hdh'd' .H'dhd'
 |
|
| Rubik's Cube |
|
5- La singularité
L'Unicorn possède une singularité redoutable: l'état untwist !!
Pour fixer cette singularité on fait en deux étapes:
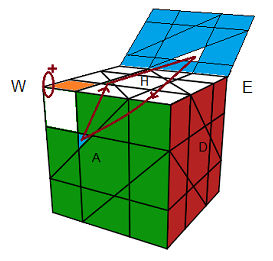
1) Pivoter le sommet:
(HAG)
+ = WH²EH² .W'H²E'H² .WH²E'H² .W
2) Remettre les co-sommets en place par la formule :
{
HAG}<->{
HPD} = (AHA'H)
5
 |
|
(HAG)+ = WH²EH² .W'H²E'H² .WH²E'H² .W
|
|
On remet en place les co-sommets par la formule:
{
HAG}<->{
HPD} = (AHA'H)
5
 |
|
| {HAG}<->{HPD} = (AHA'H)5 |
|
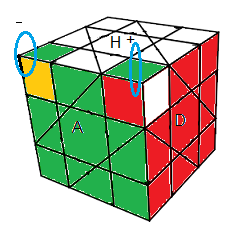
Si on a le sommet (HDA) à pivoter on passe au sommet (HAG) par la formule :
(HAG)
-(HDA)
+ = (D'BDABA') .H'(AB'A'D'B'D)H
 |
 |
| (HAG)-(HDA)+ = (D'BDABA') .H'(AB'A'D'B'D)H |
Et huup laaa !!! |
1 [2]
Accueil
DMJ: 06/02/2024





















