Résolution du Super Skewb

Notation:

Les centres seront notés entre parenthèses :
(H)aut, (B)as, (A)vant, (P)ostérieure, (G)auche, (D)roite.

Les rotations
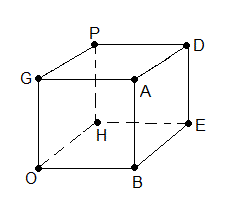
Voici les rotations (par rapport aux sommets):
(HDA) = A, (HPD) = D, (HGP) = P, (HAG) = G
(BAD) = B, (BDP) = E, (BPG) = H, (BGA) = O
G = tourner 120° le sommet Gauche dans le sens horaire.
G' = tourner -120° (dans le sens contraire) le sommet Gauche
^tH = tourner le cube entier 90° suivant la face H, abrégé : tourner le cube suivant H
^tH' = tourner le cube entier -90° suivant la face H, abrégé : tourner le cube suivant H'
^tH² = tourner le cube entier 180° suivant la face H, abrégé : tourner le cube suivant H²

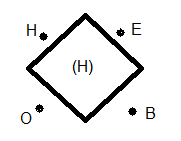
rotations par rapport aux sommets	rotations B,O,H,E autour du centre (H)

Rotation O	Rotation B

Rotation H	Rotation E

rotation tH

REMARQUE : Ces 4 rotations B,O,H,E se passent autour du centre (H)aut
La résolution se fait alors exactement comme le Skewb Ultimate. On va choisir la face Haut=blanc, Avant=vert une fois pour tout .

A- Ranger les 4 sommets Haut

On selecte un centre pour le centre Haut, pour nous c'est le centre blanc
On commence d'abord par ranger correctement les 4 sommets-Haut en tenant compte de l'orientation du centre Haut.
Utilisez les rotations B,O,H,E pour placer
A^- = [B'O'] pour orienter.
Mémo: préparer(B'), placer(O'), pivoter(B), remettre(O)
G^- = [BO] pour orienter.

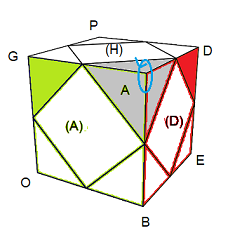A- = [B'O']

B- Placer les centres

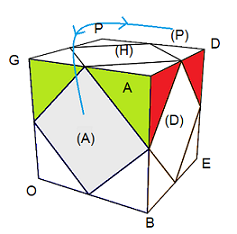
On place d'abord le centre (P) par : (A)<->(P) = [OH'] , si (P) n'est pas bien orienté, on l'oriente avec [OH']².
Puis on place le centre (D) par : (G)<->(D) = [BO'] , si (D) n'est pas bien orienté, on l'oriente avec [BO']².
On place les centres restant , avec les 2 formules suivantes:
1. (A)->(G)->(B) = [B'E'][HE]
2. (A)->(B)->(D) = [H'E'][HO]

(A)<->(P) = [OH']	(A)<->(B),(G)<->(D) = [BO']

(A)->(G)->(B) = [B'E'][HE]	(A)->(B)->(D) = [H'E'][HO]

C- Orienter les centres

Formules pour pivoter (pivoter=°) les centres:
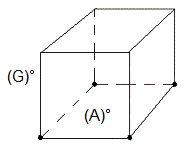
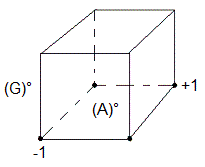
(A)°(G)° = [HE']²[EB']²

On a 2 centres à tourner (180°)

(A)°(G)° = [HE']²[EB']²

Remarque : Si les 2 centres à pivoter ne sont pas en position (A) et (G), il suffit de les déplacer (A)->(G)->(B), les pivoter puis les remettre à leur emplacement origine

D- Orienter les sommets Bas

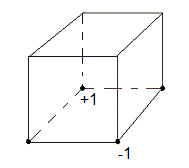
[BO']⁴ = B=1,O=1,H=-1,E=-1

Deux cas se présentent:

Cas1 : 2 sommets à pivoter (ils sont opposés) (BPG), (BAD):
(BAD) A=couleur Bas, (BPG) G=couleur Bas
TENIR B=1 puis appliquez [BO']⁴ , on passe alors au cas 4 sommets à pivoter

Cas2: 4 sommets à pivoter:
les 2 sommets-adjacents (même couleur Bas) en Bas-Droite.
(BAD) D=couleur Bas, (BDP) D=couleur Bas
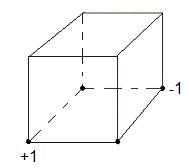
TENIR B=-1,O=-1 puis on appliquez [BO']⁴

Cas1: Pivoter 2 sommets TENIR B=1 appliquez [BO']4 ==> Cas2	Cas2: Pivoter 4 sommets TENIR B=-1,O=-1 appliquez [BO']4

Commentaire

L'algorithme est basé sur le commutateur [BO'], en effet le comportement de [BO'] est vraiment intéressant
[BO'] = (A)<->(B),(G)<->(D) , permute les centres (et pivote aussi les sommets Bas) , on voit donc
[BO']² = (A)°(B)°(G)°(D)° , remet les centres à leur place mais les pivote, à partir de là on peut bricoler pour pivoter 2 centres, c'est assez simple il suffit de changer le référentiel
[HE']² [EB']² = (A)°(G)° (ou encore [BO']² [OH']² = (D)°(P)°)

[BO']² pivote les centres et aussi les sommets Bas, comme les sommets ont 3 orientations alors que les centres en ont deux , donc
[BO']⁴ = pivote 4 sommets-Bas.

c'est exactement comme [DH] pour le Rubik's Cube

Remarque :
[EB']² = ^tH' [HE']² ^tH

d'autres formules :

[HE']2 [EB']2 [O'B]4 [H'O]4	[BO']4 [H'O]4

[HE']2 [EB']2	[O'B]4 [H'O]4

1 [2]

Accueil

DMJ: 20/09/2024