Résolution du Squarebik
21
Sep
2024
La résolution se fait classiquement comme un Rubik's Cube, mais avec quelque formules différentes:
1. Finir le Bas : ranger les arêtes , puis les sommets
2. Finir l'équateur
3. Finir le Haut
-Placer les sommets
-Pivoter les sommets
-Glisser les arêtes
NOTE : Les formules ne doivent avoir que les rotations : H,D,B.
Les cubes qui n'utilisent que 3 rotations sont très intéressants
-Fused : H,D,A ==> adjacent (3 rotations adjacents)
-Squarebik : H,D,B ==> serie (3 rotations en serie)
Notation:
 |
 |
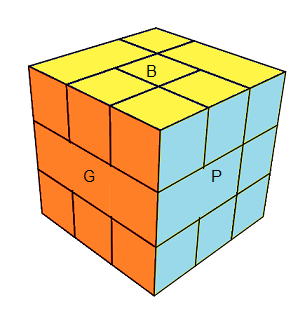| recto |
verso = recto + tD² tH' |
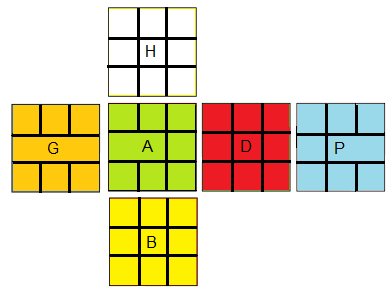
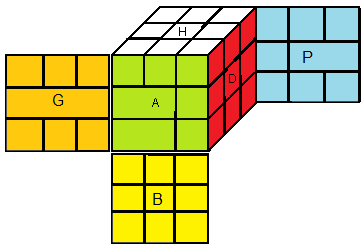
On va nommer les faces et les couleurs:
(H)aut=(b)lanc , (B)as=(j)aune , (A)vant=(v)ert , (P)ostérieur=(k)lein , (G)auche=(o)range , (D)roite=(r)ouge.
Les rotations
A = tourner 90° la face Avant dans le sens des aiguilles d'une montre.
A' = tourner 90° dans le sens contraire
A² = tourner 180°
Remarque : Si vous n'arrivez pas à faire des rotations c'est que vous êtes trompé dans les formules !!
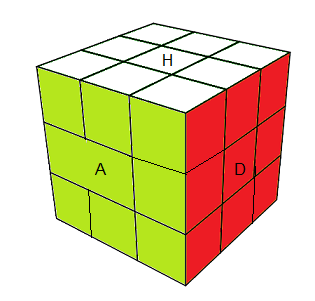
Dans les dessins, la face Avant porte la couleur
verte, et on voit le Haut (
blanc) et la Droite (
rouge).
On écrit (HA) pour désigner le arête Haut-Avant ou (HDA) le sommet Haut-Droite-Avant
Le point '.' ou les parenthèses '(', ')' qui se trouvent dans les formules sont là pour faciliter la lecture c'est tout!!!
Finir le Bas
Ranger les 4 arêtes Bas
-On range les arêtes Bas (on fait la Croix-Bas) :(BP),(BG),(BA),(BD) très facile
 |
|
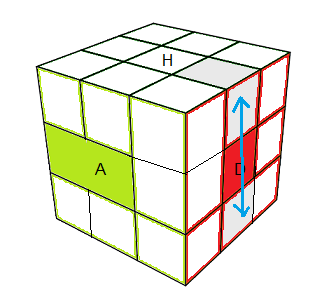| (HD)<->(BD) = D² |
|
Ranger les sommets Bas
c'est très facile aussi
-On range les sommets Bas: placer [DH], et orienter [DH]²
 |
 |
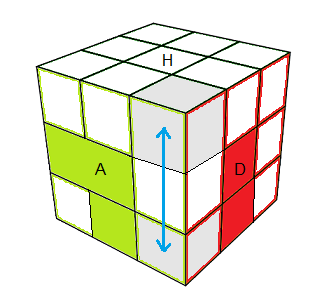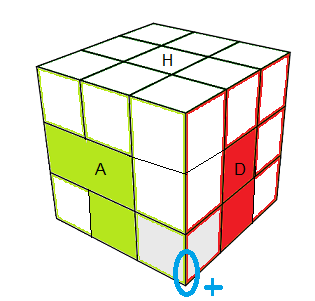| (HDA)<->(BAD) = [DH] |
(BAD)+ = [DH]² |
Finir l'équateur
Il y a seulement deux arêtes à ranger (AD) et (PD) ça fait avec la formule suivante:
(HG)->(HD)->(HA) = D²HDHD'(H'D')²HD' = E
 |
 |
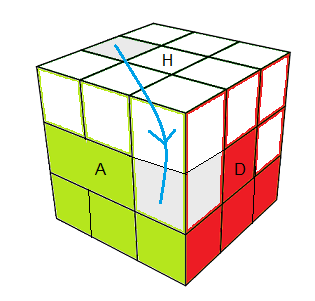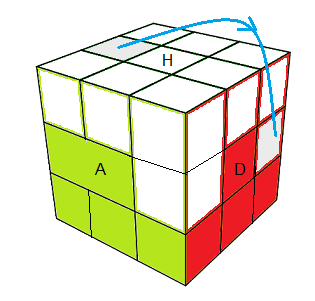| (HG)->(AD) = DED' |
(HG)->(PD) = D'ED |
Finir le Haut
Placer les sommets Haut
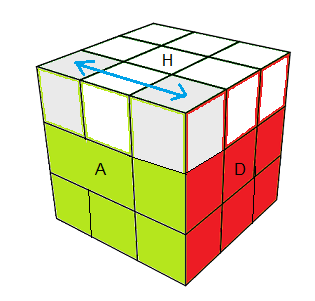
Une nouvelle formule (HAG)<->(HDA) = H²DHD²B .D'HDB' .(D'H')² D'H
 |
|
| (HAG)<->(HDA) = H²DHD²B .D'HDB' .(D'H')² D'H |
|
Pivoter les sommets Haut
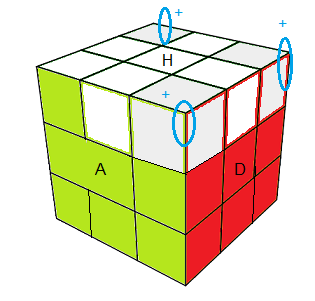
La formule exige qu'on doit avoir un seul sommet "bon" en Haut, donc on se débrouille pour remplir cette condiction
 |
|
| (HDA)+(HPD)+(HGP)+ = DHD'H .DH²D'H² |
|
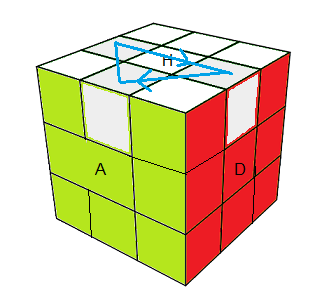
Glisser les arêtes Haut
 |
 |
| (HG)->(HD)->(HA) = D² HDHD' (H'D')² HD' |
et hup la !! Squarebik |
1 [2]
Accueil
DMJ: 21/09/2024
