Résolution du Son-Mum

Notation:

On va nommer les faces:
H(aut), B(as), A(vant), P(ostérieure), G(auche), D(roite).
h(aut-intérieur), b(as-intérieur), a(vant-intérieur), p(ostérieure-intérieur), g(auche-intérieur), d(roite-intérieur).

Et on fixe le Cube ainsi:
H(aut)=b(lanc), B(as)=j(aune), A(vant)=v(ert), P(ostérieur)=k(lein), G(auche)=o(range), D(roite)=r(ouge)

Les rotations
H = tourner 90° la face Haut dans le sens horaire.
H' = tourner 90° dans le sens contraire
H² = tourner 180°
h = tourner 90° la face hant-intérieur dans le sens horaire (h = H*H').
h₀ = tourner 45° la face hant-intérieur dans le sens horaire.
h'₀ = tourner -45°.

H	h

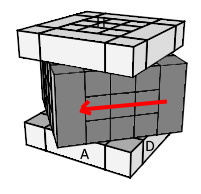h0 = 45°

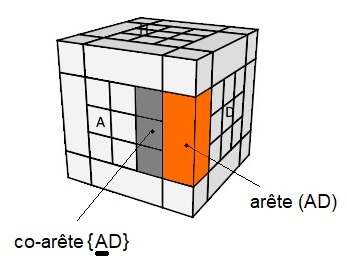
Notation

Le point '.' ou les parenthèses '(', ')' qui se trouvent dans les formules sont là pour faciliter la lecture c'est tout!!!

A- Remettre sous la forme cubique

C'est la partie la plus difficile car souvent le Cube est bloqué, on dispose très peu de rotations, donc la première chose à faire c'est débloquer le maximum de rotations possibles, pour ça on se fait aider par des règles et des formules et du feelling car il n'y a pas vraiment d'algorithme:

Règles :
- Les arêtes occupées dans les centres doivent être verticales
- Les co-arêtes doivent être aussi verticales

Formules :
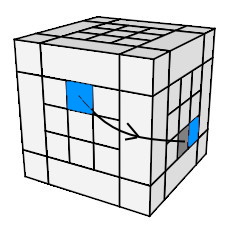
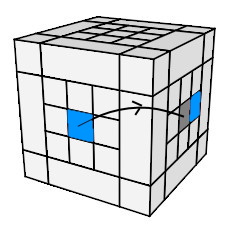
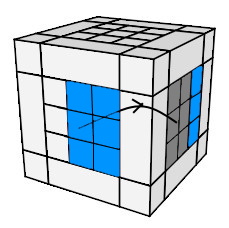
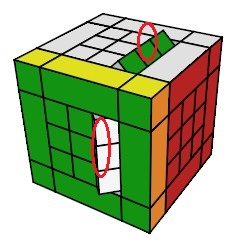
- Pivoter l'arête à 45°:
(AD)° = h₀ .dHd'. h'₀ H'
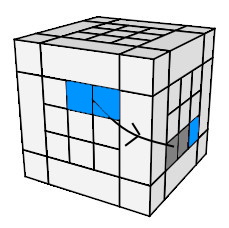
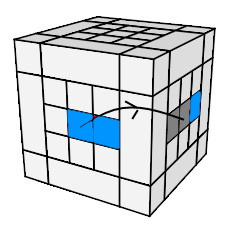
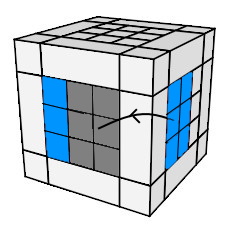
- Remettre les centres dans leur camp:
(HA)->(A) = h'₀ DH'D' h₀
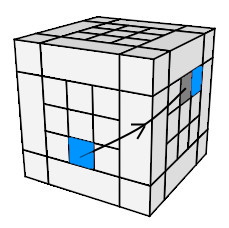
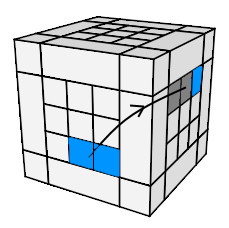
- Pivoter les co-arêtes:
{AD}° {HD}° = (a₀da'₀d') A² (da₀da'₀)

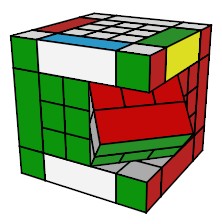Forme cubique , ce qu'on veut	(AD)° = h0 .dHd'. h'0 H'

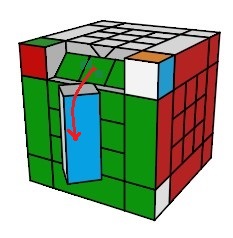(HA)->(A) = h'0 DH'D' h0	{AD}° {HD}° = (a0da'0d') A² (da0da'0)

B- Former les centres

B1: Former les 3I
Les faces (A) et (D) sont des faces de travail, une fois formé un I on le sauvegarde sur les autres faces , pour ne pas détruire ce qu'on a fait.
On utilise une seule formule
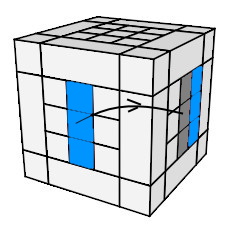
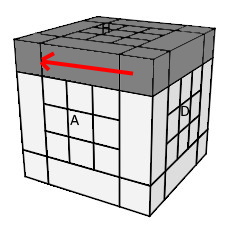
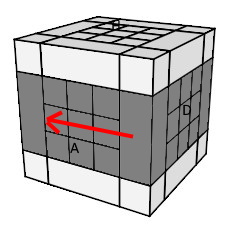
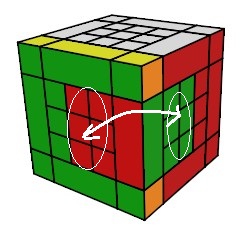
échanger les blocs :
(A)<->(D) = h₀ A² h'₀

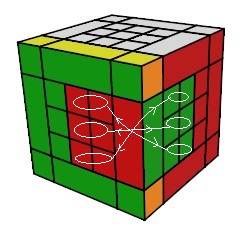h0 A² h'0	En détaille

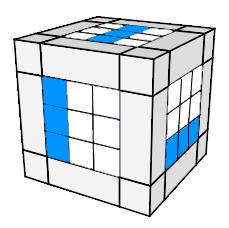Ce qu'on veut

On utilise aussi la symétrie

B2: Former les centres
On utilise une seule formule
h₀ A² h'₀



On fait la même chose pour les autres couleurs.

B3: Les deux derniers centres
Le plus dur est les deux derniers centres à former
On utilise une seule formule
h₀ A² h'₀

Voici les 4 situations à savoir:

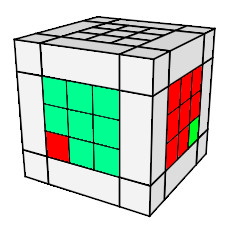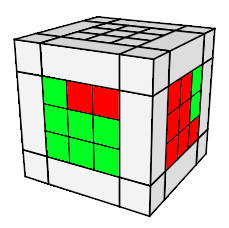1) h0 A² h'0	2) h0 A² h'0

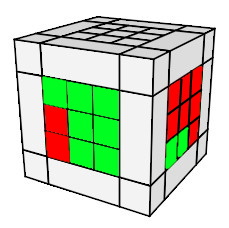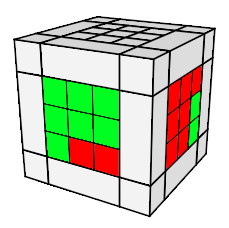3) h0 A² h'0	4) h0 A² h'0

B4: Ranger les centres
Tout d'abord il faut connaitre la couleur des faces, pour nous c'est:
H(aut)=b(lanc), B(as)=j(aune), A(vant)=v(ert), P(ostérieur)=k(lein), G(auche)=o(range), D(roite)=r(ouge)

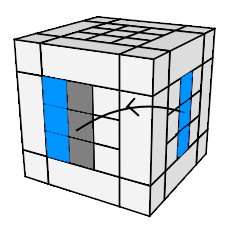
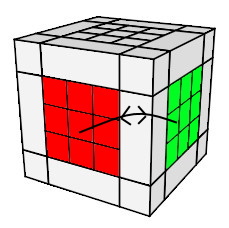
On place les centres en respectant les couleurs: On échange les centres par:
(A)<->(D) = (h₀ A² h'₀) A² (h₀ A² h'₀) D² (h₀ A² h'₀)

(A)<->(D) = (h0 A² h'0) A² (h0 A² h'0) D² (h0 A² h'0)

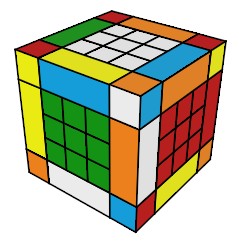
C- Resoudre le Son-Mum comme un 3x3x3

On resoud le Son-Mum normalement comme un 3x3x3 (ignorez les problèmes de parités, on les verra plus tard).

Comme un 3x3x3

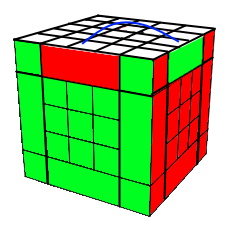
D- Le problème de parité

Le Son-Mum peut gènèrer une parité terrifiante: Permuter 2 arêtes (ou 2 sommets c'est pareil)
(HA)<->(HD) = ([AD']h₀ .[D'A]h₀)⁴ [AD']h₀

(HA)<->(HD) = ([AD']h0 .[D'A]h0)4 [AD']h0 Puis résoudre de nouveau le Cube.

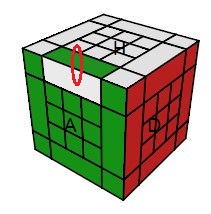
E- Le problème d'orientation

Il y a un problème d'orientation
Pour ce problème, il n'y a rien à faire il faut apprendre par coeur les formules c'est tout !!!

a0 (Dh')4 H' (hD')4 H a'0

F- Commentaire

L'état de parité s	L'état monoflip t

L' état s est bien un état de parité et non un état singulier, de même l' état t est un état monoflip et non un état singulier, en effet les rotations standards du Son-Mum sont:
Rotations standards (rotation de base) : {H,B,A,P,G,D}
Rotations non-standards (rotation de non-base) : h, h₀, d, d₀, a, a₀, ...
Comme le Rubik's Cube , le Son-Mum a la même loi de parité, les même lois d'orientations. L'état s viole la loi de parité, l'état t viole la loi des flips.
La cause de la parité ou de l'état monoflip provient du fait qu'on a utilisé les rotations non-standards comme h₀A²h'₀, pour mélanger le Cube, d'où pour fixer la parité on doit utiliser des rotation non-standards.

1 [2]

Accueil

DMJ: 06/02/2024