Résolution du Quarter Cube/Constrained

1- Notation

A(vant) , P(ostérieur) , H(aut) , B(as) , G(auche) , D(roite).

Les rotations
A = tourner 90° la face Avant dans le sens des aiguilles d'une montre.
A' = tourner 90° dans le sens contraire

Le point '.' et les parenthèses '(', ')' qui se trouvent dans les formules sont là pour faciliter la lecture c'est tout!!!

Analyse du puzzle

Le Quarter autorise seulement les rotations alternatives, c'est à dire par exemple pour la face Avant une fois A et une fois A' mais pas A², Celà nous oblige de trouver de nouvelles formules pour déplacer et pivoter les pièces.

Phase A: Placer les arêtes

On commence par mettre le cube en position START, c'est à dire tous les faces doivent avoir la rotation 90° , et on garde cette position durant la résolution.

On va placer toutes les arêtes (sans se soucier de leur orientation, on verra ça plus tard)

A1 : Placer les arêtes
On va placer les arêtes, c'est assez simple, on utilise la formule:
(HP)->(HA)->(HD) = A[DH]A'
On commence par le Bas, l'équateur puis le Haut

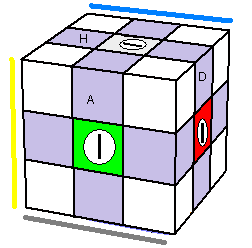
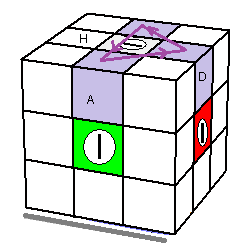
Ce qu'on veut	(HP)->(HA)->(HD) = A[DH]A'

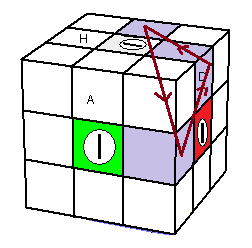
(AD)->(HD)->(HP) = [DH]

REMARQUE IMPORTANTE:
En plaçant les arêtes on a utilisé la formule A[DH]A', c'est un 3-cycle-arête (permutation paire).
On pourrait se demander si c'est possible d'avoir deux arêtes à permuter ? La réponse est NON, en effet dans la position START, les faces ont subi les rotations du genre AA' , HH', BB', ... donc les arêtes ont subi une permutation paire, conclusion on ne peut pas avoir deux arêtes à permuter !! Notre formule place bien toutes les arêtes.

Phase B: Orienter les arêtes

Les arêtes sont bien placées, maintenant on va les orienter
C'est la partie la plus intéressante de la résolution. J'ai mis longtemps pour trouver la formule ci-dessous qui pivote les 2 arêtes

Tenir le cube comme il le faut :
Pivoter les arêtes (HA) et (HD)
1. A[DH]A'
2. G[HA]G'
3. D[HP]D'

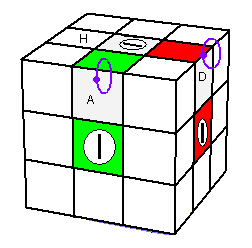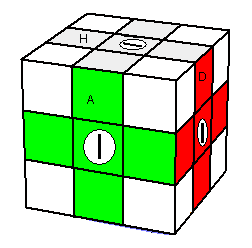
Ce qu'on veut	1. A[DH]A' 2. G[HA]G' 3. D[HP]D'

Phase C: Placer les sommets

On place les sommets grâce à la formule:
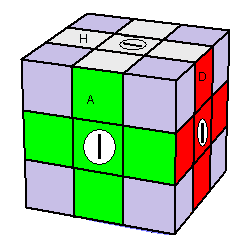
(BPG)->(HPD)->(HGP) = [DH] .G[HD]G'
On peut aussi utiliser [DH]³ = (HDA)->(BAD)

Ce qu'on veut	(BPG)->(HPD)->(HGP) = [DH] .G[HD]G'

[DH]3 = (HDA)->(BAD)

Phase D: Orienter les sommets

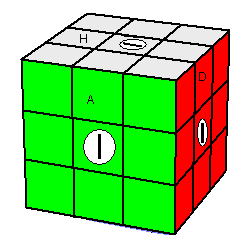
On oriente les sommets grâce à la formule:
(BPG)⁺(HGP)^- = [DH]² .G[HD]²G' , Postérieur -> Gauche

Ce qu'on veut	(BPG)+(HGP)- = [DH]² .G[HD]²G'

Commentaire

En réalité la résolution n'utilise que 4 formules (les autres sont là pour vous faciliter la vie), ces 4 fotmules correspondent aux 4 étapes de la résolution:

1. Placer les arêtes: A[DH]A'
2. Pivoter les arêtes: A[DH]A' .G[HA]G' .D[HP]D'
3. Placer les sommets: [DH] .G[HD]G' = [[DH],G]
4. Pivoter les sommets: [DH]² .G[HD]²G' = [[DH]²,G]

Le plus dur c'est le point 2.
En effet, si on range (bien placé et bien orienté) toutes les arêtes, mais quand on arrive à la dernière croix (ranger les 3 arêtes Haut) on tombe sur un problème vicieux ...
- Soit les 3 arêtes sont bien placées mais mal orientées
- Soit les 3 arêtes bien orientées mais mal placées
On tourne donc en rond !!!
Il faut donc trouver une formule qui glisse les arêtes c'est à dire qui les déplace mais sans changer leur orientations ou une formule qui pivote 2 arêtes, ces formules existent mais elles utilisent des carrés A² , H² .... d'où la difficulté
Il m'a fallu plusieurs heures pour trouver la formule: A[DH]A' .G[HA]G' .D[HP]D' qui pivote deux arêtes et n'utilise que les rotations alternatives.

Les MOD

Avec Constrained on peut facilement fabriquer les MOD: Constrained4bik et Constained2bik

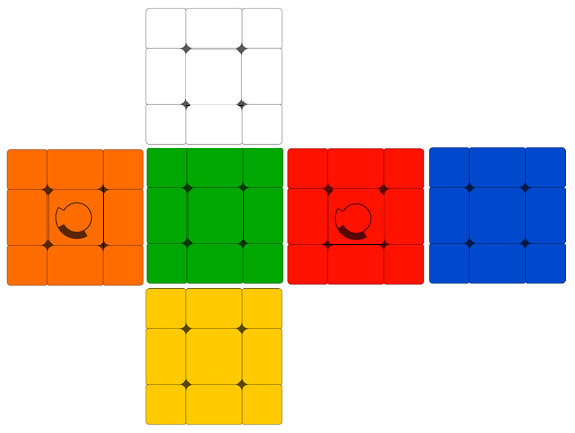
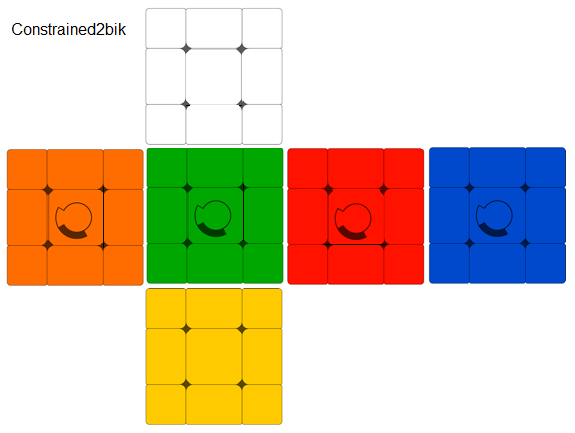
Constrained4bik config	Constrained2bik config

Constrained4bik	Constrained2bik

Pour la résolution de ces cubes, il faut tenir le cube de telle sorte quu'une face Rubik soit le Haut. Et pour permuter deux arêtes-Haut on utilise la formule A[DH]A'H = (HG)<->(HP) c'est possible puisque le Haut est une face Rubik.

1 [2]

Accueil

DMJ: 27/01/2023