Résolution du Pyramorphinx

1- Notation

Les rotations
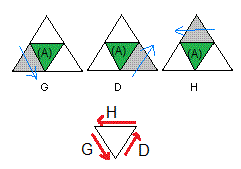
G(auche), D(roite), H(aut)
G = tourner 90° dans le sens des aiguilles d'une montre.
G' = tourner -90° (dans le sens contraire)
G² = tourner 180°


Attention: Les rotations sont difficiles, il ne faut pas perdre de vue le "triangle" autour du quel on fait les rotations.

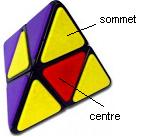
On écit (BGA) pour désigner le sommet Bas-Gauche-Avant
(BGA)° = pivoter le sommet (BGA)
Le point '.' ou les parenthèses '(', ')' qui se trouvent dans les formules sont là pour faciliter la lecture c'est tout!!!

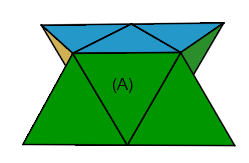
Former un tétraèdre

Remettre sous la forme un tétraèdre
Le but c'est d'arriver à cette forme >< puis une rotation H on obtiendra le tétraèdre.


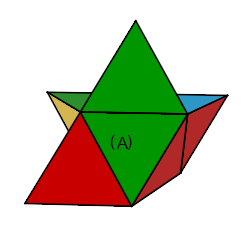
Il y a 5 formes différentes, on applique les formules correspondantes suivant le cas:

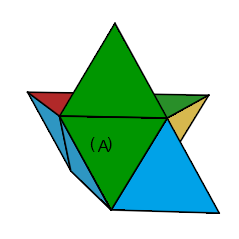Oreille-g: G	Oreille-d: D'

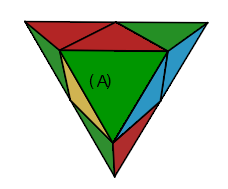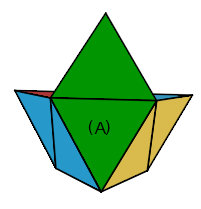Chapeau: DH'	Fusé: D²

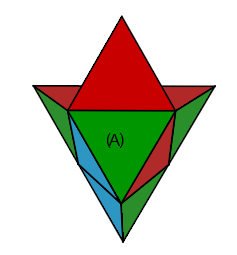Cassé: H'G'

Ranger les sommets

Voici la formule pour pivoter le sommet (BDG): [DG']²
(BDG)° = [DG']² = DG'D'G .DG'D'G

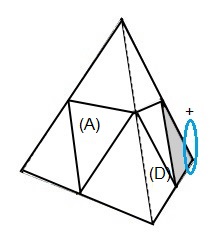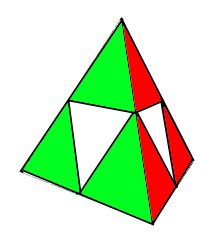
Ce qu'on veut	(BDG)° = [DG']² = DG'D'G .DG'D'G

Ranger les centres

On va permuter les centres.
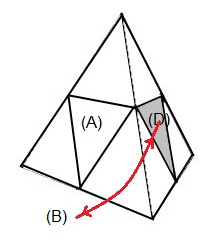
permuter: (B)<->(D) = (HG²D'H²G')³

(B)<->(D) = (HG²D'H²G')3	et huppp laaaa!!!

1 [2] 3

Accueil

DMJ: 23/09/2022