Résolution du Pocket

1-Notation

La première chose à faire c'est qu'il faut nommer les faces et fixer le Cube:
(H)aut=(b)lanc , (B)as=(j)aune , (A)vant=(v)ert , (P)ostérieur=(k)lein , (G)auche=(o)range , (D)roite=(r)ouge.

Les rotations faces
A = tourner 90° la face Avant dans le sens horaire.
A' = tourner -90°
A² = tourner 180°

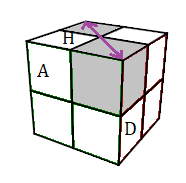
Dans les dessins, la face Avant porte la couleur verte, et on voit le Haut (blanc) et la Droite (rouge) .
Le point '.' ou les parenthèses '(', ')' qui se trouvent dans les formules sont là pour faciliter la lecture c'est tout!!!

A- Finir le Bas

On commence par placer les sommets-Bas
On va placer les sommets-Bas dans l'ordre suivant: (BAD), (BDP), (BPG) et (BGA) :

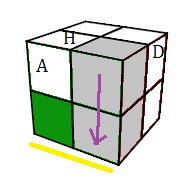
1. Choisissez un sommet-Bas (jaune) , placez le en (HDA), puis descendez le en (BAD)
Descendre: (HDA)->(BAD) = [DH]
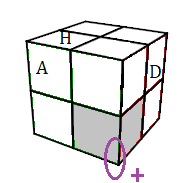
Si le somme (BAD) n'est pas orienté, on le oriente tout de suite par la formule: Pivoter: (BAD)⁺ = [DH]²
2. ^tH tourner le Cube entier suivant H, on cherche alors le sommet qui a les couleurs Bas et Avant
3. Revenez au point 1.

Remarque: si le sommet cherché est en Bas on le remonte avec [DH]

(HDA)->(BAD) = [DH]	(HAD)+ = [DH]²

Mémo:
DHD'H': Monter(D)/Placer(H)/Descendre(D')/Revenir(H')
[DH]² ==> Descendre + remonter = pivoter

B- Finir le Haut

On commence par placer les sommets, puis on les oriente

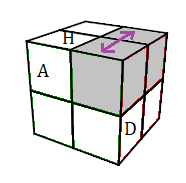
Echanger deux sommets : (HDA)<->(HPD) = [DH]A'H'A
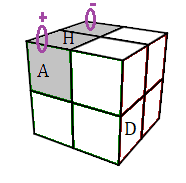
Pivoter deux sommets : (HAG)⁺(HGP)^- = [DH]² .G'[HD]²G

(HDA)<->(HPD) = [DH]A'H'A	(HAG)+(HGP)- = [DH]² .G'[HD]²G

Résumé :

1. Descendre un sommet: [DH]
2. Pivoter un sommet-Bas: [DH]²
3. Permuter 2 sommets Haut-Droite: [DH]A'H'A
4. Pivoter 2 sommets Haut-Gauche: [DH]² .G'[HD]²G

Formules supplémentaires

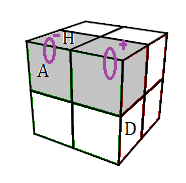(HGP)<->(HDA) = θ = A[DH]A'.H	(HAG)-(HDA)+ = (D'BD.ABA') . H'(AB'A'.D'B'D)H

Bricolage

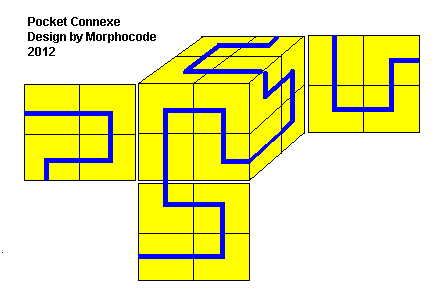Pocket Connexe

1 [2]

Accueil

DMJ: 08/05/2023