Résolution du Megaminx

Notation:

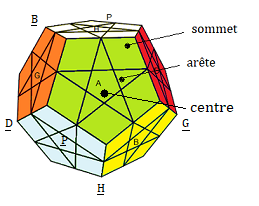
Prenez votre Megaminx et posez le sur la table, comme ceci:.


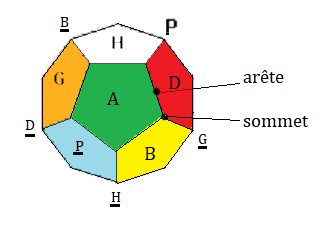
On va nommer les faces utilisées dans les formules:
H(aut) , B(as), A(vant) , P(ostérieur) , G(auche) , D(roite),
H(aut-opposé), D(roite-opposé).

Les rotations
A = tourner 72° la face Avant dans le sens horaire.
A' = tourner -72° (dans le sens antihoraire)
A² = tourner 144° dans le sens horaire

On écit (HA) pour désigner le arête Haut-Avant ou (HDA) le sommet Haut-Droite-Avant
(HA)° = pivoter le arête (HA)
(HDA)° = pivoter le sommet (HDA)
Le point '.' ou les parenthèses '(', ')' qui se trouvent dans les formules sont là pour faciliter la lecture c'est tout!!!

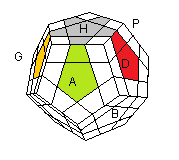
A- Faire l'étoile prolongée

On va chosir une face pour commencer, par exemple la face blanc-clair.
Attention: La couleur des faces latérales doit correspondre avec l'étoile (comme la Croix pour le Rubik's Cube)...

Ce qu'on veut

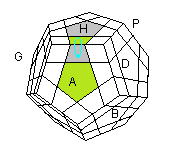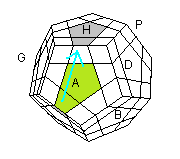
A²	A . H' DH

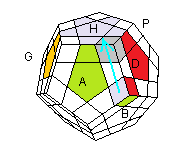
B- Placer des sommets

On monte le sommet (BAD) en (HDA): Descendre(D')/Prendre(B')/Monter(D)

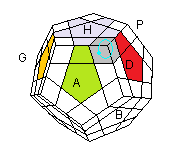(BAD) -> (HDA) = D'B'D	(HDA)° = D' BD . ABA'

C- Ranger tous les arêtes-équateur-bas

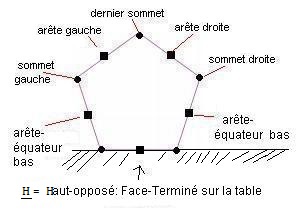
On va ranger toutes les arêtes-équateur-bas (arête au dessus de chaque sommet de la Face-Terminée) en utilisant les formules:
[HD][H' A' ] ou [H' A' ][HD]
Pour cela, il faut tenir le Megaminx de telle sorte que la Face-Terminée (pour nous c'est blanc-clair) soit = face Bas. Cette étape ressemble à l'étage "équateur" du Rubik's Cube

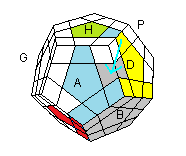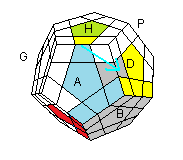(HD)->(AD) = [H' A' ][HD]	(HA)->(AD) = [HD][H' A' ]

D- Faire les 5 faces adjacentes à la Face-Terminée

Cette partie n'est pas compliquée, mais elle est un peu longue. Tenir le Megaminx de telle sorte que la Face-Terminée (pour nous c'est blanc-clair) soit = H(aut-opposé), autrement dit poser la Face-Terminée sur la table !
Choisir une face adjacente à la Face-Terminée:

1. Ranger le sommet gauche:

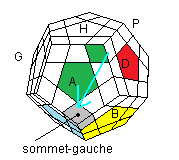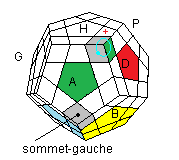H'A'² H A²	H'A' H² A

2. Ranger le sommet droite:

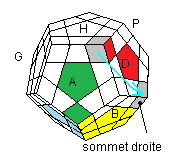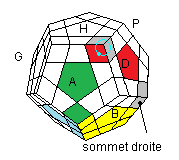HD²H' D'²	HDH'² D'

C'est facile, le principe est simple: On dégage puis on 'monte':
-si l'orientation est bonne on prend la pièce , sinon on pivote la pièce

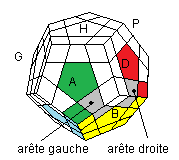
3. Ranger l'arêtes gauche, et l'arête droite:
C'est aussi facile, on s'arrange pour pouvoir utiliser [HD][H' A' ] ou [H' A' ][HD] (et la conjugaison)


REMARQUE :
I. Il faut bien positionner l'arête avant d'appliquer les formules: [HD][H' A' ] ou [H' A' ][HD]
II. S'il l'arête se trouve à l'équateur-haut: on la délogge vers le Haut par [HD][H' A' ]

4. Ranger le dernier sommet:
Pareil: on dégage puis on monte: si l'orientation est bonne on 'recueille', sinon on 'pivote'.

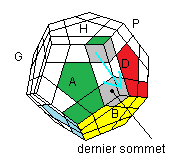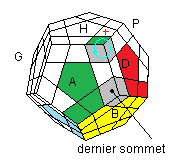HDH'D'	HDH'²D'

Mémo:
Recueillir: Dégager(H)/Monter(D)/Prendre(H')/Descendre(D')
Pivoter: Dégager(H)/Monter(D)/Pivoter(H'²)/Descendre(D')

E- Mettre tous les arêtes de l'équateur haut

Mettre toutes les arêtes de l'équateur haut avec les formules:
[HD][H' A' ] ou [H' A' ][HD]

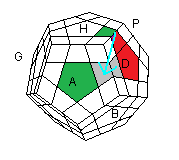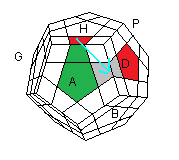
(HA)->(AD) = [HD][H' A' ]	(HD)->(AD) = [H' A' ][HD]

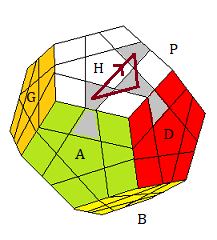
F- Ranger les arêtes Haut

Placer les arêtes, pour cela on utilise la formule : A[HD]A' = (HA)->(HP)->(HD)
On essaie d'avoir 2 adjacentes

A[HD]A' = (HA)->(HP)->(HD)

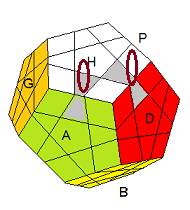
Pivoter 2 arêtes : (HA)⁺(HD)⁺ = A[HD]HA'HA . H³ A'
On essaie d'avoir 3 adjacentes

(HA)+(HD)+ = A[HD]HA'HA . H3 A'

G- Ranger les sommets Haut

I. D'abord on veut seulement placer les sommets, l'orientation on verra.
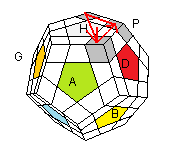
Permutation (circulaire) des 3 sommets:
(HDA)->(HPD)->(HBP) = [HA]. P'[AH]P
On commence par avoir 2 sommets adjacentes. Puis placer les 3 autres

(HDA)->(HPD)->(HBP) = [HA]. P'[AH]P

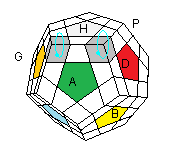
II. On va maintenant orienter les 2 sommets-adjacents. Monter les 2 couleurs Avant vers Haut

(HAG)°(HDA)° = (D' BDABA') .H'(AB' A' D' B' D)H	Eh hup laaaa!!!!

Formules supplémentaires

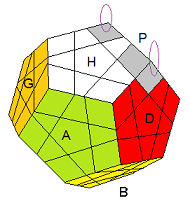
Voici 2 formules pour pivoter les sommets
1. [HA]². P'[AH]²P
2. [HA]² .B'P'[AH]²PB

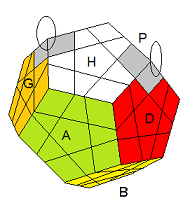[HA]² .P'[AH]²P	[HA]² .B'P'[AH]²PB

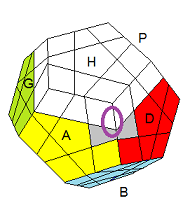DH²D'H² .DH²D'H .[A'H']

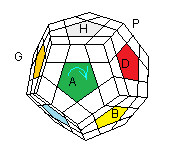
Super Mégaminx

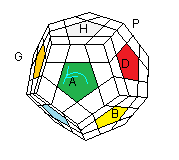
Si les centres de votre Mégaminx sont orientés , voici 2 formules pour les pivoter.

(A)+ = (H'² D²H².AD'²A)3	(A)- = (D²H'² D'².A' H²A')3

1 [2]

Accueil

DMJ: 30/10/2024