Le groupe du Floppy

Analyse

Avant d'aller plus loin, précisez bien la notion "permutation", et la notion "orientation"
- Une permutation, c'est qu'il y a un déplacement en cycles des pièces
- Une orientation, c'est qu'il y a plusieurs façons que la pièce se place (se loge) dans un emplacement.

Prenons notre Floppy Cube et analysons le:

Floppy Cube	D = / (lire slash)

Examinons une rotation de base par exp D (on note D=180° aulieu de D²) on a:

1. Le sommet (blanc,rouge,vert,bleu) se déplace à (BAD) mais il a une seule façon de se loger dans (BAD), donc les sommets se déplacent, mais pour un emplacement donné un sommet a une seule façon de se loger dedans !! donc pour les sommets il n'y a pas d'orientation, on a affaire à S₄

2. Pour l'arête (vert,rouge,bleu) elle ne bouge pas ! donc pas de permutations, par contre elle a 2 façons de se placer dans (AD) . Les arrêtes ne se déplacent pas mais elles ont 2 orientations, donc pour les arêtes on a affaire à Z₂⁴

Finalement pour le Floppy Cube on a affaire à quelque chose comme ça:
G⁺ = S₄ x Z₂⁴

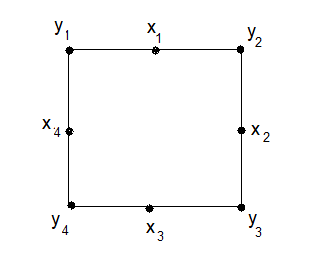	nom des pièces

Mais les déplacements des sommets ont des contraintes, par ex le sommet (blanc,rouge,vert,bleu) se déplace à (BAD) uniquement en permutation impaire ! et à (BGA) uniquement en permutation paire .... Les sommets ne peuvent pas se déplacer comme ils veulent. Pour aller d'un endroit à un autre ils se déplacent soit uniquement en permutations paires soit uniquement en permutations impaires mais pas les deux.
Soit L=la longeur du chemin (le nombre n'arêtes)
sig(u) = (-1)^L (*)

Pour l'orientation des arêtes, on a des valeurs alternées 0->1 et 1->0 quand on permute deux sommets donc si on pose
x₁ l'arête corespond à la rotation H
x₂ l'arête corespond à la rotation D
x₃ l'arête corespond à la rotation B
x₄ l'arête corespond à la rotation G

Alors on a
H(x)=(1-x₁,x₂,x₃,x₄ )
D(x)=(x₁,1-x₂,x₃,x₄ )
B(x)=(x₁,x₂,1-x₃,x₄ )
G(x)=(x₁,x₂,x₃,1-x₄ )

NOTE : Pour compter le nombre d'orientations des arêtes c'est simple, il suffit de compter le nombre d'étiquettes bleues sur la face verte. En effet on peut marquer 0 sur la face verte (donc 1 sur la face bleue) et prendre la couleur dominante est verte.

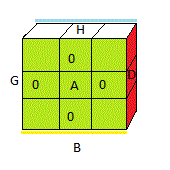	Les facettes marquées

La loi interne de G⁺

On voudrait définir une loi '.' de composition sur G⁺ , et si on observe bien les rotations de base H, D, B, G on trouve la loi de composition:
e.H = (u,x)
u=(y₁,y₂)
x=(1-x₁,x₂, x₃,x₄)
(u,x)(v,y) = (uv, v(x))
Les éléments de G se sont donc les éléments de G⁺ qui vérifient la loi (*) càd
G = { (u,x) / sig(u) = (-1)^L }
On rappelle que G c'est l'ensemble des états produits par M = < G, D, H, B >
Ce qui donne |G| = (4!/2) x 2⁴ = 192 on divise par 2 car les permutations doivent respecter la loi (*)

Pourquoi la contraine (*) nous fait perdre la moitié des permutations ? parce que pour aller d'un point à l'autre on a soit que la longueur paire soit que la longueur impaire donc dans tous les cas on n'a que la moitié des permutations c'est pourquoi il faut diviser 4! par 2 : 4!/2

Commentaire

On pourait comparer le groupe de Floppy au groupe du Pyraminx, ou du Pocket.
En effet les 2 ont un apparence semblable

Floppy:

1. G⁺ = S₄ x Z₂⁴
2. Loi de composition: (u,x)(v,y) = (uv, v(x))
3. Pas de loi de twists
4. Pas de loi de flips
5. Loi de permutations: sig(u) = (-1)^L

Pyraminx:

1. G⁺ = S₆ x Z₂⁶
2. Loi de composition: (u,x)(v,y) = ( uv, x+u(y) )
3. Pas de loi de twists
4. Loi de flips: ∑ x_i = 0 (mod 2)
5. Loi de permutations: sig(u) = 1

[1]

Accueil

DMJ: 21/09/2024