Résolution du Golden Cube

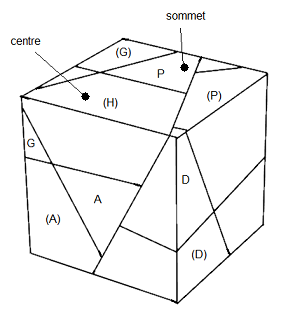
1- Notation

Les centres seront notés entre parenthèses :
(H)aut, (B)as, (A)vant, (P)ostérieure, (G)auche, (D)roite.

Les sommets seront notés sans parenthèses :
sommets Haute: A=Avant, G=Gauche, P=Postérieure, D=Droite.
sommets Bas: B=Bas, O=Ouest, H=Haut, E=Est

Les rotations
Voici les rotations (par rapport aux sommets):
A, G, P, D
B, O, H, E
B = tourner 120° le sommet Bas dans le sens horaire.
B' = tourner -120° (dans le sens anti-horaire) le sommet Bas

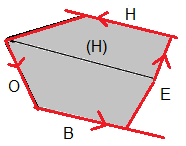Nom des pièces	rotations autour du centre Haut

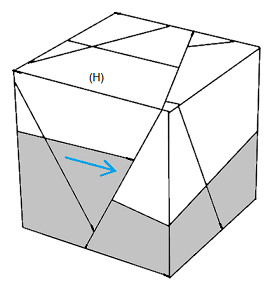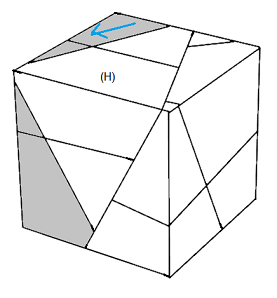Rotation B	Rotation O

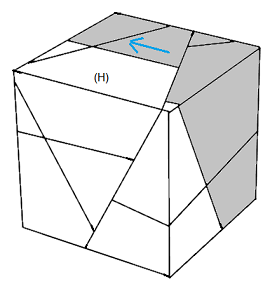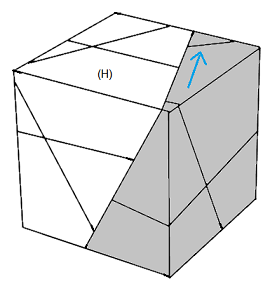Rotation H	Rotation E

REMARQUE : Avant de faire des rotations il faut se placer en position START.
Ces 4 rotations se passent autour du centre (H)aut

On va choisir le centre (H)aut comme indique la figure.

A- Ranger les 4 sommets Haut

On va chercher la pièce qui désigne le centre Haut (H), ensuite on va ranger les quatre sommets Haut autour de leur centre (H). On commence par ranger le sommet A="Triangle équilatéral" , puis D, G et P en utilisant les rotations B, O, H, E.
On les oriente tout de suite si nécessaire

Sommet-Haut A : triangle équilatéral
Sommet-Haut D : tour Eiffel
Sommet-Haut G: un coin arrondi
Sommet-Haut P : trapèze isocèle

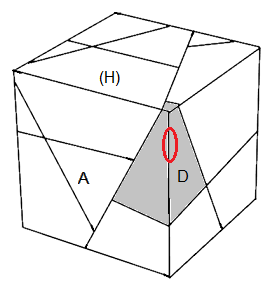pivoter sommet D-: [B'O'] = B'O'BO

MEMO : Pour pivoter un sommet voici le "Mémo":
D^- = placer(B')/pivoter(O')/remettre(B)/revenir(O)

Une fois les sommets Haut sont bien placés , les sommets Bas sont automatiquement bien placés donc on n'a pas besoin de connaitre les sommets Bas !!

NOTE IMPORTANTE :
Pour le Golden Cube de MEFFERT (faux Golden Cube), le triangle équilatéral est un triangle quelconque !! donc 3 orientations !!

Le Golden Cube de MEFFERT, pas de singularité (faux Golden Cube)

Le sommet A="Triangle équilatéral" est particulièrement difficile à orienter correctement,
A = +1 ==> la pièce dépasse légèrement la surface
A = -1 ==> la pièce point vers la droite

donc il faut absolument sûr qu'il est bien orienté avant de placer les centres. A l'origine ce triangle est un triangle équilatéral qui rend le Golden Cube la possibilité de gènérer une singularité. Mais la production en masse de Meffert a un bug qui supprime cette possibilité (vraiment dommage) car le centre A est en réalité un triangle quelconque qui a donc 3 orientations !!!

B- Placer les centres

Il faut absolument connaitre la forme des centres pour pouvoir les placer.

a) On range (bien placé et bien orienté) d'abord le centre (P) : (A)->(P): [OH'] = OH'O'H
s'il n'est pas bien orienté, on le oriente avec [OH']² .

b) On range le centre (D) : (G)->(D): [BO'] = BO'B'O
s'il n'est pas bien orienté, on le oriente avec [BO']²

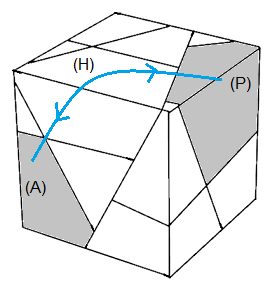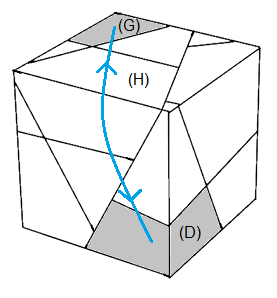(A)->(P): [OH']	(G)->(D): [BO']

c) On place les centres restant avec 2 formules :
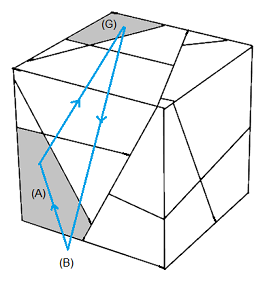
(A)->(G)->(B) = [B'E'][HE]
(A)->(B)->(D) = [H'E'][HO]
Permutation circulaire de 3 centres.

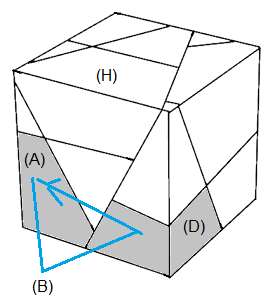(A)->(G)->(B) = [B'E'][HE]	(A)->(B)->(D) = [H'E'][HO]

C- Orienter les centres

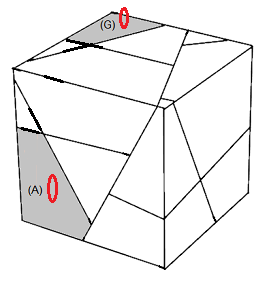
Formules :
(A)°(G)° = [HE']²[EB']²

On a 2 centres à pivoter 180°

(A)°(G)° = [HE']²[EB']²

Remarque : Si les 2 centres à pivoter ne sont pas en position (A) et (G), il suffit de les déplacer (A)->(G)->(B), les pivoter puis les remettre à leur emplacement origine

D- Orienter les sommets Bas

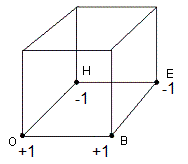
C'est la partie la plus délicate, car il faut reconnaitre l'orientation d'un sommet: 1 ou -1 pour pouvoir tenir le Cube correctement.
Posons K = [BO']⁴
K pivote les 4 sommets Bas comme indique la fig ci-dessous

Action de K sur le Cube: [BO']4 = (B,O,H,E) = (1,1,-1,-1)

Deux cas se présentent:

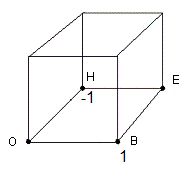
- Lorsqu'on a 2 sommets (opposés) à pivoter , on tient le Cube de telle sorte que B=1, puis appliquez K, le but c'est de "détruire" ces 2 sommets , on passe alors au cas 4 sommets à orienter.

Tenir le Cube comme ça B=1

1. Tenir B=1 : le "+1" à Droite
2. Appliquer [BO']⁴

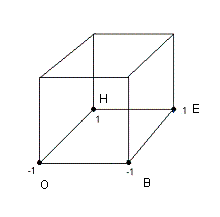
- Lorsqu'on a 4 sommets à pivoter, on tient le Cube de telle sorte que (B,O)=(-1,-1) puis appliquez K.

Tenir le Cube comme ça (B,O)=(-1,-1)

1. Tenir (B,O)=(-1,-1) : les "-" devant
2. Appliquer [BO']⁴

Graphe de sortir
Tout cela suppose qu'on reconnait l'orientation d'un sommet 1 ou -1 mais si on ne sait pas on peut quand même s'en sortir aveuglement !

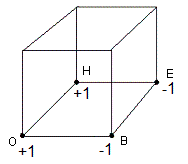
posons Z = [OH']⁴

Action de Z sur le Cube: [OH']4 = (B,O,H,E) = (-1,1,1,-1)

==> 2 sommets à pivoter on applique Z
==> 4 sommets à pivoter on applique K
Le graphe si-dessous vous permet de s'en sortir (aveuglement). Si on a de la chance on applique seulement K , le pire des cas c'est KZZKK.

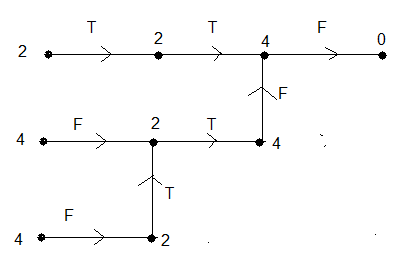Graphe de sortir

La singularité

Grâce à la pièce triangle équilatéral T, ce sommet est invariant par pivotement, ça peut générer une singularité-sommet : pivoter un seul sommet S !!
il est assez subtil de fixer cette singularité
PRINCIPE : On veut pivoter S avec le triangle équilatéral T.

==> 3 sommets à pivoter : On applique K pour avoir 1 sommet à pivoter

Un sommet S à pivoter :
1) On va pivoter S avec le triangle-equilatéral T. On tient le Cube de telle sorte que:
a) T et S soient des sommets Bas
b) Le sommet T=B est opposé de S=H
2) appliquer la formule : [BO']⁴ [H'O]⁴


Autres formules pour fixer les singularités :

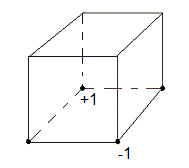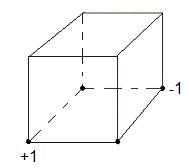[BO']4 [H'O]4	[O'B]4 [H'O]4

1 [2]

Accueil

DMJ: 09/09/2024