Résolution du Dino Cube

Notation

Rotations
On va nommer les faces et fixer le Cube:
H(aut)=b(lanc) , B(as)=j(aune) , A(vant)=v(ert) , P(ostérieur)=k(lein) , G(auche)=o(range) , D(roite)=r(ouge).

Les faces seront notées entre parenthèses: (H) = face Haut, (A) = face Avant, ...
Les sommets seront notés sans parenthèses: sommet A (rotation A)
(HDA) = A, (HPD) = D, (HGP) = P, (HAG) = G
(BAD) = B, (BDP) = E, (BPG) = H, (BGA) = O
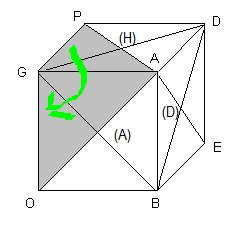
On n'a besoin que 2 rotations, comme indique la fig ci-dessous
G(auche), A(vant).
G = tourner dans le sens des aiguilles d'une montre (120°).
G' = tourner dans le sens contraire (-120°)

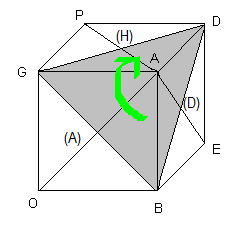
Rotation G	Rotation A

A- La formule magic

C'est qui est vraiment étonnant , c'est qu'on a besoin d'une seule formule pour résoudre le Dino Cube !!!
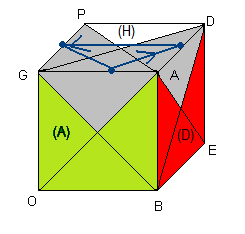
(HA)->(HD)->(HG) = [GA'] = GA'G'A , cette formule déplace 3 arêtes et laisse invariant le reste du cube comme indique la fig ci-dessous

(HA)->(HD)->(HG) = [GA'] = GA'AG'

B- Finir la face Haut

On va donc utiliser la formule [GA'] ou son invers [A'G] pour placer les arêtes, une fois les arêtes placées elles seront automatiquement bien orientées !!

Comme dans l' Edge Only

1. On sélecte une couleur pour le Haut: pour nous c'est Haut=blanc
On va placer successivement les arêtes Haut (HA), (HD), (HP), (HG)
2. On place une arête-Haut en (HA), par exp: (bv)
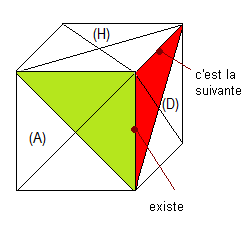
3. On cherche l' arête suivante (HD):
- En (HD) on suppose c'est (bx) par exemple, (x=une couleur)
- Si l'arête (vx) existe alors l'arête (bx) est la suivante, sinon il faut la changer
4. Une fois l'arête suivante est trouvée, ^tH Tourner le cube suivant H
5. Revenir en 3.

Note : pour x on a deux solutions : x=rouge ou x=orange

(HA)->(HD)->(HG) = [GA'] = GA'AG'

On finit ainsi le Haut.

C- Finir le cube

Une fois le Haut fini, avec la même formule :
==> On place les arêtes-Equateur (^tD : tenir le cube: face-finie(Haut) => Postérieur)
==> Puis les arêtes-Bas (^tD² : tenir le cube: Bas => Haut)

Résumé :
La résolution du Dino Cube est vraiment très simple, on n'utilise qu'une seule formule:
- Déplacer 3 arêtes: (HA)->(HD)->(HG) = [GA'] = GA'G'A
- L'orientation sera automatique quand les pièces sont bien placées !!

Commentaire

A) La résolution donne deux solutions :
1) H(aut)=b(lanc) , B(as)=j(aune) , A(vant)=v(ert) , P(ostérieur)=k(lein) , G(auche)=o(range) , D(roite)=r(ouge).
2) H(aut)=b(lanc) , B(as)=j(aune) , A(vant)=v(ert) , P(ostérieur)=k(lein) , G(auche)=r(ouge) , D(roite)=o(range).

B) Dans l'introdution je disais que le Dino Cube a une propriété très curieuse, faites donc l'expérience suivante.

1. Prenez votre Dino résolu
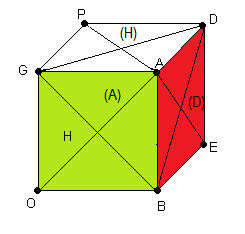
2. Placez le solidement sur la table comme indique la fig1 ci-dessous :
H(aut)=b(lanc) , B(as)=j(aune) , A(vant)=v(ert) , P(ostérieur)=k(lein) , G(auche)=o(range) , D(roite)=r(ouge).
3. Appliquez la formule cachée: X = DAD'.GAE'.D'PH'.O

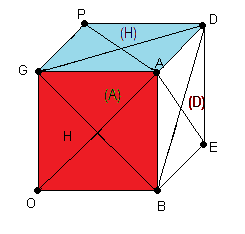
fig1	fig1 • (DAD'.GAE'.D'PH'.O) = fig2

Vous verrez que la couleur des faces a changé ! et pourtant vous n'avez pas bougé le cube ! c'est la propriété "Trou de ver" : on change d'endroit (= l'entourage, le cadre) sans bouger physiquement !
On a changé :
H(aut)=k(lein) , B(as)=v(ert) , A(vant)=r(ouge) , P(ostérieur)=o(range) , G(auche)=j(aune) , D(roite)=b(lanc).
En fait on a: G<->D

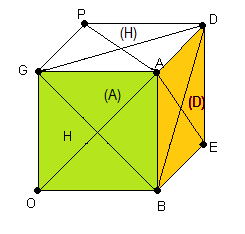
Voici une autre formule, plus longue mais plus simple à retenir qui produit le même phénomène.
Y = DGBH.A'P'E'O'.DGBH
On a changé :
H(aut)=j(aune) , B(as)=b(lanc) , A(vant)=k(lein) , P(ostérieur)=v(vert) , G(auche)=r(ouge) , D(roite)=o(range).
En fait on a: G<->D

fig1 • (DGBH.A'P'E'O'.DGBH) = fig3

On pourrait dire que le Dino Cube possède 2 univers parallèles et on passe de l'un à l'autre par ces deux formules X ou Y.
Deux univers :
1) H(aut)=b(lanc) , B(as)=j(aune) , A(vant)=v(ert) , P(ostérieur)=k(lein) , G(auche)=o(range) , D(roite)=r(ouge).
2) H(aut)=b(lanc) , B(as)=j(aune) , A(vant)=v(ert) , P(ostérieur)=k(lein) , G(auche)=r(ouge) , D(roite)=o(range).

B) Remarque !! :On peut classer les états du Dino suivant la D-symétrique (D=le groupe du déplacement du cube) ce groupe possède 24 éléments
et comme le Dino donne 2 solutions, on a 2|G|/24 = 19958400 D-classes, chaque D-classe a 12 éléments

d'ailleurs GAP nous donne: gap_dino.txt

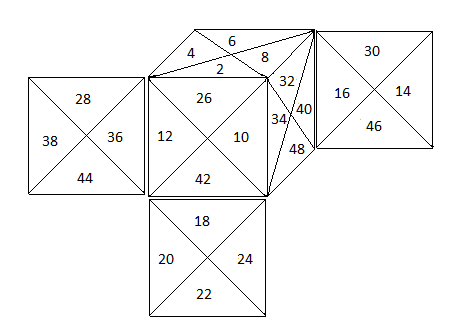
Les stickers numérotés

Permutations associées au rotations de base: H,B,A, ...
p_H = (14,44,22) (38,20,46)
p_B = (18,10,48)(42,34,24)
p_A = (2,32,10) (26,8,34)
p_P = (4,38,30) (28,14,6)
p_G = (2,12,28)(26,36,4)
p_D = (8,30,40)(32,6,16)
p_O = (18,44,12)(42,20,36)
p_E = (24,40,46)(48,16,22)

Λ = < p_H, p_B, p_A, p_P, p_G, p_D, p_O, p_E >

|Λ| = 239500800
G = A₁₂
|Λ| = |G| = 239500800

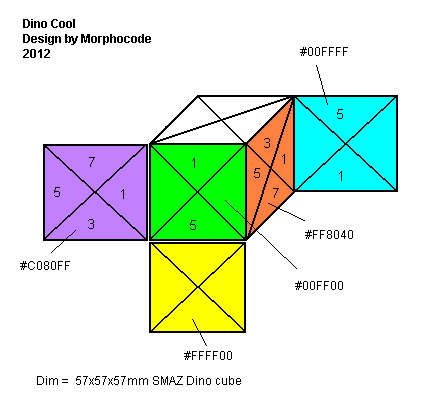
Dino Cool !!

Voici un nouveau jeu de stickers qui donne votre Dino 2 propriétés très étonnantes.


- Ce Dino Cool ne donne une seule solution (contrairement pour un Dino normal, toujours 2 solutions)

- Trouver l'arête blanc-1, puis tenir le cube de telle sorte que Haut=blanc, Avant=1
Alors : la some des nombres: Haut + Bas + Equateur(Avant,Postérieur) = un nombre pair !
Autrement dit:
Arête Haut = (HA)+(HD)+(HP)+(HG) = U (compter les chiffres en Haut)
Arête Bas = (BA)+(BD)+(BP)+(BG) = V (compter les chiffres en Bas)
Arête équateur = (AG)+(AD)+(PD)+(PG) = W (compter les chiffres Avant et Postérieur)
Alors U+V+W = toujours pair !!!

1 [2]

Accueil

DMJ: 08/06/2026