Résolution du Curvy Copter
08
Mai
2013
Méthode les sommets d'abord
La résolution se fait à partir de la forme cubique et pratiquement comme l'Helicopter. Les arêtes jouent le rôle de référence,
ce sont elles qui déterminent la couleur des faces.
Comme la résolution se fait à partir de la forme cubique on pourrait limiter les mélanges ainsi:
==> Soit des mélanges cubiques, càd on part de la forme cubique et on arrive à la forme cubique.
==> Soit on limite les rotations non-standards au maximum 10
Voici quelques formules non-standards pour les mélanges cubiques:
1. d'²Ad² PGA d²Pd'²
2. d'²Ad² PGP d'²Ad²
3. e'g'AgeA
4. doAo'd'A
 |
|
| Copter |
|
{
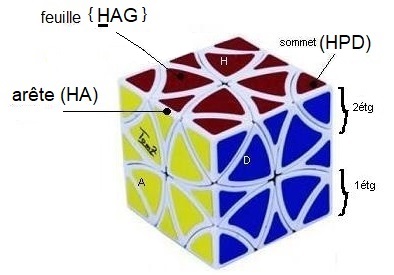
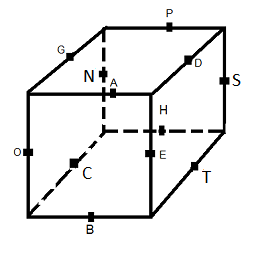
HAG} = la feuille H adjacente au sommet (HAG)
1- Notation
On va nommer les 12 rotations (correspondant aux 12 arêtes) :
(HA)=A(vant), (HP)=P(ostérieure), (HG)=G(auche), (HD)=D(roite)
(AG)=O(uest), (AD)=E(st), (PG)=N(ord), (PD)=S(ud)
(BA)=B(as), (BP)=H(aut), (BG)=C(gauChe), (BD)=T(droiTe)
 |
|
| Rotations |
|
Les rotations
Les rotations se font suivant les arêtes à 180°:
A = tourner l'arête (HA) 180° dans le sens des aiguilles d'une montre.
A' = tourner l'arête (HA) 180° dans le sens contraire
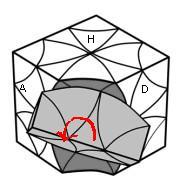
Rotations non-standards (cachées)
a = tourner l'arête (HA) 60° dans le sens des aiguilles d'une montre.
a' = tourner l'arête (HA) -60°.
 |
 |
| d |
e' |
Attention!! Toutes les rotations (standards) sont à 180°. Pour les rotation non-standards (60°) , veillez que les pièces soient bien alignées
A- Ranger toutes les arêtes
C'est très facile , il suffit de les pivoter pour les mettre sur la même couleur,
c'est la couleur des arêtes qui détermine la couleur des faces. Et pendant la résolution veillez que les arêtes soient toujours bien rangées
B- Finir les sommets
Les couleurs des sommets sont répèrées par les
arêtes.
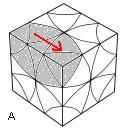
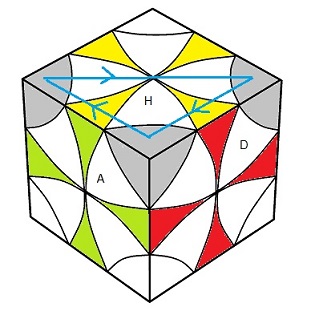
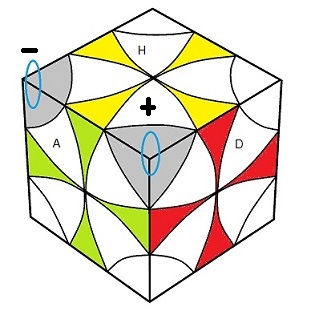
Rien de compliquer, on place les sommets avec: (HAG)->(HPD)->(HDA) = (DA)²
Puis on les pivote avec: (HAG)
-(HDA)
+ = (DA)² .G(DP)²G ; la couleur Avant monte vers le Haut
On commence par isoler les sommets
==> Si on tombe dans la parité, on utilise les formules de parité qui se trouve plus loin.
 |
 |
| (HAG)->(HPD)->(HDA) = (DA)² |
(HAG)-(HDA)+ = (DA)² .G(DP)²G |
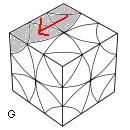
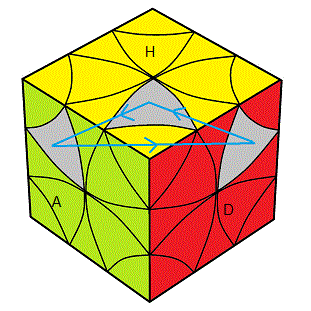
C- Finir les feuilles
On commence par placer les feuilles par {
HDA} -> {H
AG} -> {HP
D} = (DEAE)²
 |
|
| {HDA} -> {HAG} -> {HPD} = (DEAE)² |
|
1)
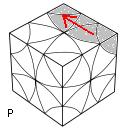
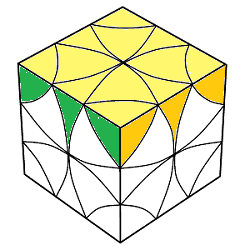
Finir le Bas
 |
|
| finir Bas |
|
2)
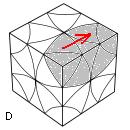
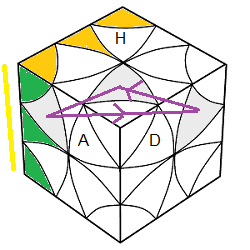
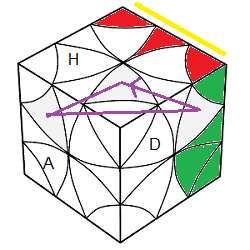
On essaie de finir le 1er étage : On tient le cube: le Bas à Gauche (pour les feuilles haut) ou à Postérieur (pour les feuilles bas).
 |
 |
| le Bas à Gauche |
le Bas à Postérieur |
 |
|
| finir 1er étage |
|
D- Problème de parité
Le Curvy Copter possède une loi de parité et une loi d'orientation :
Soit k le nombre de pivotements (à 180°) des arêtes, par définition la direction des arêtes est:
dir(arêtes) = (-1)
k
==> Loi de parité : sig(sommets) = sig(feuille_meme_orbite)
==> Loi d'orientation : dir(arêtes) = sig(sommets)
On a un problème de parité c'est quand les sommets ne sont pas en phase avec les feuilles.
Il y a un problème de parité c'est quand le cube a été mélangé avec des rotations non-standards a,g,p,... à 60°
Dans ce cas pour fixer la parité on est obligé d'utiliser les rotations non-standards , voici les formules pour fixer ces parités
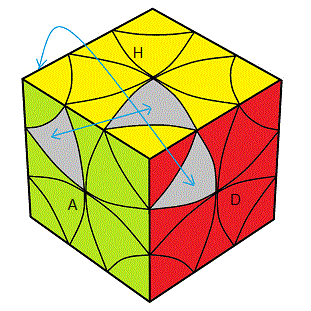
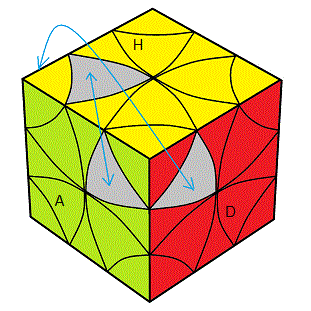
** Permuter 2 feuilles du même orbite et 2 feuilles des orbites différents
 |
 |
| (HDA, HAG) (HDA, HAG) = doAo'd'A |
(HDA, HAG) (HDA, HAG) = e'g'AgeA |
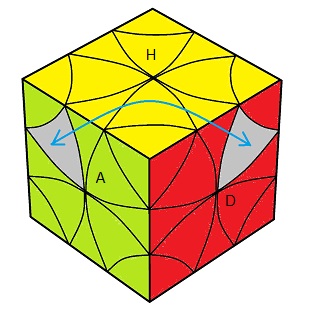
** Permuter 2 feuilles du même orbite
 |
 |
| (HAG, HPD) = DG .(doAo'd'A) .GD |
(HAG,HDA) (HAG,HDA) = (doAo'd').(e'g'Age) |
REMARQUE: Pour parler du "problème de parité" il faut préciser les rotations standards (les rotations de base), et montrer (à partir de ces rotations)
qu'on a une loi de parité. Pour le Curvy Copter on a 12 rotations standards:
{A,G,P,D,....} rotation d'arêtes à 180°.
Et on voit qu'on a la loi des phases, par ex pour la rotation A on a les sommets et les feuilles d'une ordibte sont en phase.
La cause de la parité s'explique par le fait que les feuilles changent de leur orbite quand on utilise les rotations non-standards {a,g,p,d,...} à 60°
1 [2]
Accueil
DMJ: 26/09/2024