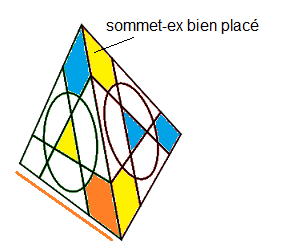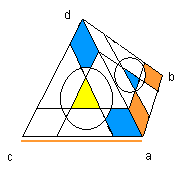Solution du Crazy-Tetrahedron-Mercure

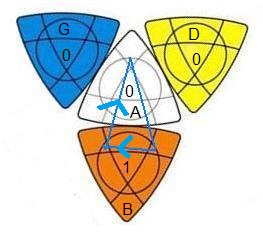
1- Notation

CONSEIL : Si votre cube a des couleurs différentes alors il vaut mieux convertir les couleurs dans les dessins en couleurs de votre cube .
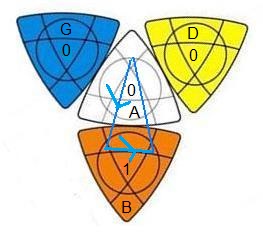
Sur mon Cube est: 0-blanc, 0-jaune, 0-klein et 1-orange

La première chose à faire c'est qu'il faut chercher les faces de valeur 0, 0-face = cercle bloqué .
Le Crazy-Tetrahedron-Mercure, possède trois 0-faces !!.

B(as)=o(range) , A(vant)=b(lanc) , G(auche)=k(lein) , D(roite)=j(aune).

Les rotations
G = tourner 120° la face Gauche dans le sens horaire.
G' = tourner -120° (dans le sens contraire)

Rotation G	Rotation D

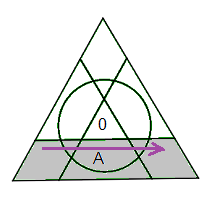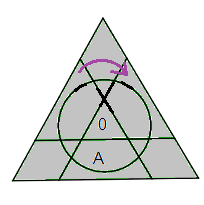Rotation B	Rotation A

Le point '.' et les parenthèses '(', ')' qui se trouvent dans les formules sont là pour faciliter la lecture c'est tout!!!

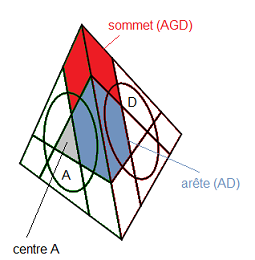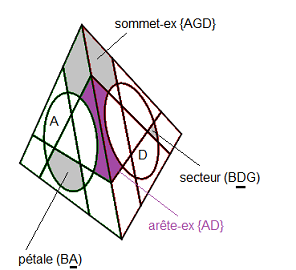
les noms des pièces

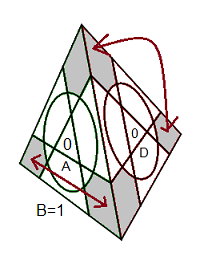
Phase 1: Placer les sommets-externes

Ce qu'on veut c'est placer correctement les sommets-externes sans se soucier de leur orientation.
Les sommets-externes sont répérables par les 3 couleurs des centres.
On met centre Bas = 1 ;(B=1)

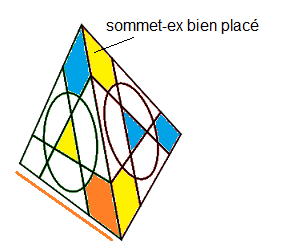centre B=1: [DG']	Sommet-externe bien placé

Phase 2: Placer les pétales

Ce n'est pas bien difficile. On place centre Bas=1 (centre orange)

[GB'] ;(B=1)	[D'B] ;(B=1)

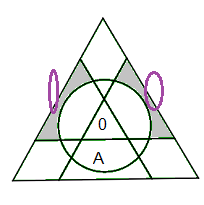
Phase 3: Ranger les arêtes-externes

On place centre Bas=1 (centre orange)
On commence par placer les arêtes-ex Bas
a) On va placer les arêtes-externes grâce à la formule suivante:
{AG}->{AD}->{PG} = [DG']
Si vous avez oublié la couleur des faces, alors répèrez la couleur grâces aux sommets
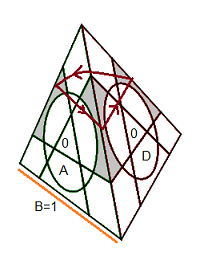
b) Orienter les arêtes-externes:
{AG}°{AD}° = [DG'][A'G]

[DG'] ;(B=1)	[DG'] [A'G] ;(B=1)

Phase 4: Placer les secteurs

C'est la partie la plus difficile, en effet il y a 12 secteurs à placer un par un et puis les formules sont vraiment longues bien que ce soit facile à retenir, il ne faut sur tout pas se tromper.

On place le centre Bas=1 ;(B=1)

secteur klein haut

1. [DG'] B[G'D]B' 2. [DG'] B'[G'D]B	1. B'[DG']B [G'D] 2. B[DG']B' [G'D]

secteur klein gauche	1) face klein à gauche 2) rotation D

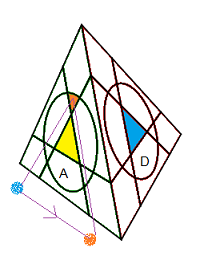secteur klein droite	1) face klein à droite 2) rotation G'

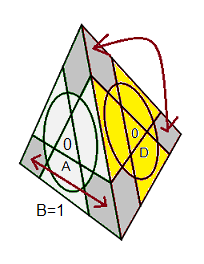
Phase 5: Ranger les sommets-externes

C'est pratiquement fini maintanant. On replace les sommets-externes (si nécessaire) puis on les oriente
On met le centre Avant=1 (A=1)
a) Placer les sommets-externes: [DG']³ avec B=1
b) Orienter les sommets-externes: [DG']² B[G'D]²B' avec A=1

[DG']3 avec B=1	[DG']² B[G'D]²B' avec A=1

Et voilà le travail!!

Commentaire

Si on observe bien on voit que l'algorithme fait un double travail, c'est la phase 1 (placer les sommets-ex) et la phase 5a (placer les sommets-ex). On pourrait donc supprimer la phase 1. Mais alors dans ce cas il arrive parfois (mais pas toujours) un phénomène bien étrange: la non-résolubilité !!. On a déjà rencontré ce genre de phénomène dans le Master Skewb pour l'algorithme 'RexCube'.

Pour bien comprendre de quoi il s'agit, on va désigner Alg^- l'algorithme sans la phase 1, et Alg l'algorithme entier avec la phase 1: Alg = 1 + Alg^-

Le phénomène est suivant:
Avec Alg^-, il arrive parfois que le cube se trouve dans un état non-résoluble (impossible de mettre les sommets-ex en place) !! donc de temps en temps ça marche, et de temps en temps ça ne marche pas !!! , cela nous mène aux questions suivantes:

1. Quelle est la cause de ce phénomène ? càd qui est ce qui fait que le cube est non-résoluble ?
2. Quelle est la probabilité de tomber dans le cas non-résoluble ?
3. Dans un état donné comment est on sûr à 100% que c'est résoluble ?
4. Dans un état donné comment est on sûr à 100% que c'est non-résoluble ?

J'avoue que j'ai du mal à comprendre ce phénomène, contrairement au problème de parité qui est plutôt facile à comprendre. Comment ça fait que parfois Alg^- résolve le cube , parfois non ? et dans quel cas on est sûr à 100% que Alg^- marche et dans quel cas on est sûr à 100% que Alg^- ne marche pas ?

A. On va analyser l'algorithme Alg^-
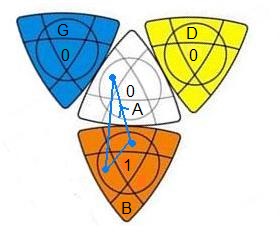
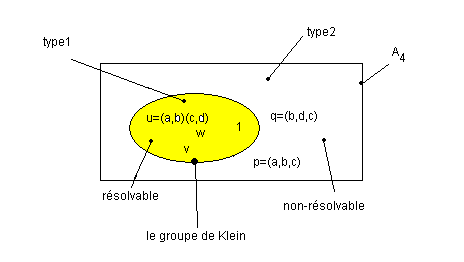
Ce qui nous intéresse ici , ce sont les 4 sommets-externes: E={a,b,c,d}. Durant la résolution on utilise les commutateurs (son inverse, la conjugaison et la puissance), ces commutateurs permutent 2 couples de sommets-ex, u = (a,b)(c,d) disons les permutations paires de type1 (les permutations paires de type2 sont p=(a,b,c) ; q=(b,d,c) etc .... les 3-cycles)
ce genre de permutation il y en a 3:
u = (a,b)(c,d)
v = (a,c)(b,d)
w = (a,d)(b,c)
un rapide calcule nous donne :

1 = identique	Les 4 sommets concernant

Pendant la résolution on utilise aussi la conjugaison, mais on tombe toujours sur u,v ou w en effet on a la formule suivante:
pup' = p(a,b)(c,d)p' = p(a,b)p' p(c,d)p'=(p(a),p(b)) (p(c),p(d)) c'est un truc de type1

B. Analysons l'état du cube
Une fois mélangé, les sommets-ex {a,b,c,d} subis une permutation paire car une rotation de base gènère une permutation paire
Cas0: 0 sommets-ex bien placé ==> possible
Cas1: 1 sommets-ex bien placé ==> possible
Cas2: 2 sommets-ex bien placés ==> impossible car la permutation doit être paire
Cas3: 3 sommets-ex bien placés ==> impossible le 4ème est forcement bien placé.
Cas4: 4 sommets-ex bien placés ==> possible
il reste donc les cas: cas0, cas1, et cas4

Et voila, maintenant nous sommes en mesure de répondre à nos questions.

Reponse4: Dans le cas1, le cube est non-résoluble en effet dans ce cas le mélange résume une permutation de la forme
p = (a,b,c) = a->b->c qui laisse fixe un sommet-ex d (sommet-ex bon), comme l'agorithme n'utilise que les permutations du type u=(a,b)(c,d)
on doit faire pu , donc si pu=1 ça signifie que
pu=1
pu=u² (car u²=1)
pu=uu
puu^-1=uuu^-1
p=u !!! imposible
car u bouge 4 sommets ne laisse fixe personne.
finalement quand on est dans le cas1 , Alg^- ne donne jamais l'état identique (impossible de placer les sommets-ex) on est sûr à 100% que le cube est non-résoluble.

En Rubik's Cube, on a [DH] qui permute 2 couples de sommets (a,b)(c,d) et on la transforme en une autre [DH]G'[HD]G en un 3-cycle (c,d,e)
on pense à priorie qu'on peut faire la même chose ici transformer (a,b)(c,d) en (c,d,e) mais c'est impossible car on n'a que 4 points !

Une remarque: si on fait pu on tombe forcement sur le type2, en effet si on tombe sur le type1 on aura une contradition:
pu=v (par exemple)
puw=vw (multiplier à droite, respecter l'ordre)
pv=vw
pvv^-1=vwv^-1
p = vwv^-1 (c'est un truc de type1 donc impossible car p est de type2)

Reponse3: Dans le cas4, et cas0 le cube est résoluble en effet dans ces cas le mélange résume à une permutation de la forme
u = (a,b)(c,d) qui permute 2 couples de sommets-ex, pour avoir l'état identique il suffit de faire u²=1 (ou v², w²)

Reponse2: on a 1/3 tomber dans le cas non-résoluble

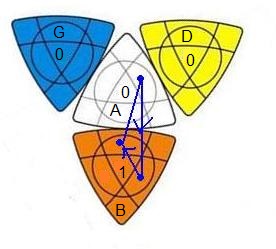
Reponse1: On a 2 types de permutations paires pour les 4 sommets: C'est quand le résultat du mélange mène l'état des sommets-ex dans le type2, Alg^- ne peut pas résolver le cube

2 types de permutations paires

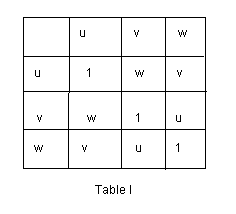
On a pu répondre à nos 4 questions grâce aux propriétés de la table I. Ces propriétés connus sous le nom de groupe, les éléments G={1,u,v,w} forme un groupe que l'on nomme Groupe de Klein
Si on observe bien on peut représenter la table I par seulement 2 symboles u et v et 2 relations:
1. u²=v²=1
2. uv=vu
autrement dit à partir de ces 2 relations on peut remplir la table I, ces relations sont en quelque sorte un .zip de la table I
c'est plus court, plus joli, mais plus concentré et difficile à comprendre. C'est sûr le tableau I c'est plus claire, plus simple à comprendre, mais c'est plus long
Finalement la résolution se fait par le Groupe de Klein !!

1 [2]

Accueil

DMJ: 21/09/2024