Résolution du Container
05
Dec
2018
Méthode le Haut d'abord
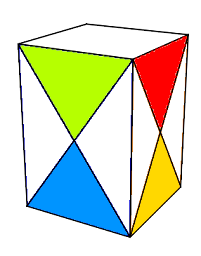
Le Container est un SuperSkewb c'est-à-dire un Skewb avec les centres orientés, mais celui-ci pose deux difficultés supplémentaires :
1. La reconaissance des centres Haut
2. Fixer la singularité-centre
Notation:
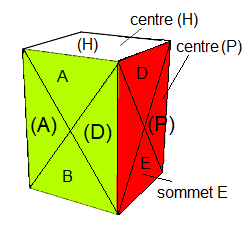
Les couleurs des faces :
H(aut)=b(lanc), B(as)=j(aune), A(vant)=v(ert), P(ostérieure)=k(lein), G(auche)=o(range), D(roite)=r(ouge),
Les centres seront notés entre parenthèses :
(H)aut, (B)as, (A)vant, (P)ostérieure, (G)auche, (D)roite.
Les sommets seront notés sans parenthèses :
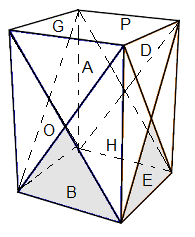
sommets Haute: A=Avant, G=Gauche, P=Postérieure, D=Droite.
sommets Bas: B=Bas, O=Ouest, H=Haut, E=Est
Les rotations
Voici les rotations (par rapport aux sommets):
A, G, P, D
B, O, H, E
B = tourner 120° le
sommet Bas dans le sens horaire.
B' = tourner -120° (dans le sens contraire) le
sommet Bas
 |
 |
| Nom des pièces |
Les sommets |
 |
 |
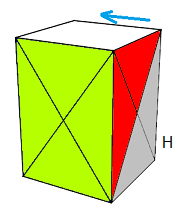
| Rotation B |
Rotation O |
 |
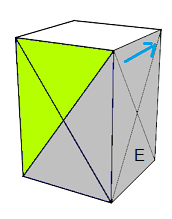 |
| Rotation H |
Rotation E |
REMARQUE : Ces 4 rotations se passent autour du centre-carré (H)aut=blanc
La résolution se fait comme le Skewb Ultimate.
A- Ranger les 4 sommets Haut
On commence d'abord par ranger
correctement les 4 sommets-Haut dans l'ordre suivant:
vert=Avant, rouge=Droite, klein=Postérieur, orange=Gauche
Utilisez les rotations B,O,H,E pour placer
A
- = [B'O'] pour orienter.
Mémo: préparer(B'), pivoter(O'), placer(B), remettre(O)
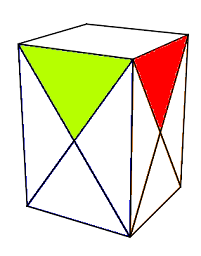 |
|
| bien rangé |
|
Il y a une difficulté, les sommets Haut et Bas sont indiscernables: par ex 2 triangles verts, et on ne sait pas quel triangle vert est pour le sommet Haut ! en fait on ne
distingue pas les sommets Haut et les sommets Bas. Quand les sommets Bas se trouvent en Haut on a:
1. Soit l'ordre des couleurs : vert, rouge, klein, orange n'est pas respecter.
2. Soit les centres Haut ne correspondent pas avec les centres Bas: on a par ex: vert-klein au lieu de vert-vert
Dans ce cas il faut replacer les sommets Haut ....
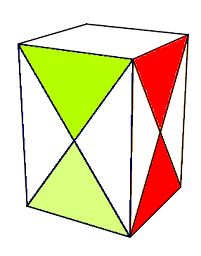 |
 |
| OK |
Erreur ==> replacer les centres Haut |
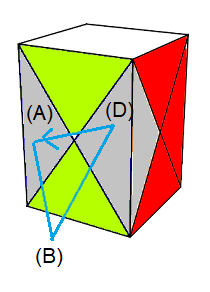
B- Placer les centres
On place les centres, avec la formule suivante:
(D)->(A)->(B) = [H'E'][HO]
En essayant d'avoir 2 centres adjacents à (H).
 |
|
| (D)->(A)->(B) = [H'E'][HO] |
|
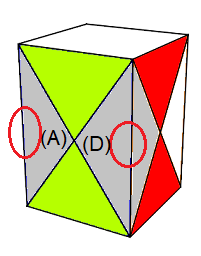
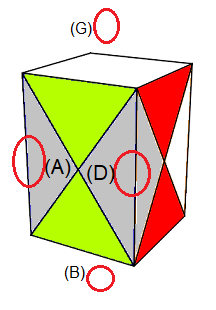
C- Orienter les centres
Formules :
(A)°(D)° = [OH']²[HE']²
(A)°(B)°(G)°(D)° = [BO']²
On a 2 possibilités: 2 , ou 4 centres à tourner (180°)
 |
 |
| (A)°(D)° = [OH']²[HE']² |
(A)°(B)°(G)°(D)° = [BO']² |
D- Les singularités
Le Container peut générer une singularite, plus précisement une singularité-centre
En effet on a 2 centres symétriques (les carrés) donc invariant par rotations, ce qui peut genérer une singularité : pivoter un seul centre.
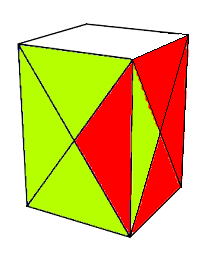 |
|
| singularité-centre |
|
Pour fixer cette singularité, ce n'est pas bien difficile, mais c'est un peu long
1. On place le centre-losange (vert,rouge) en (A) et le centre-carré (jaune) en (D) : (D)->(A)->(B) = [H'E'][HO]
2. On pivote : (A)°(D)° = [OH']²[HE']²
3. On remet les centres à leur emplacement origine : (D)<-(A)<-(B) = [OH][E'H']
E- Orienter les sommets Bas
[BO']
4 = (B,O,H,E) = (1,1,-1,-1)
Deux cas se présentent:
Cas1 : 2 sommets à pivoter (ils sont opposés) :
tenir B=1, puis appliquez [BO']
4 , on passe alors au cas 4 sommets à pivoter
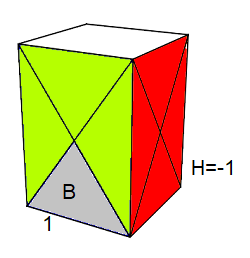
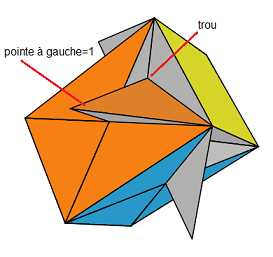
Remarque : B=1 ==> trou=sommet-triangle , pièce pointe à gauche
Cas2: 4 sommets à pivoter:
tenir (B,O)=(-1,-1) puis on appliquez [BO']
4
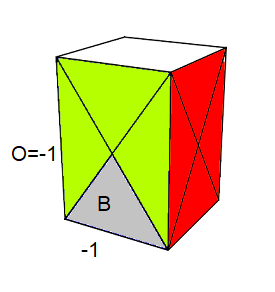
Remarque : (B,O)=(-1,-1) ==> trou=sommet-triangle , pièce pointe à droite
 |
 |
| Cas1: Pivoter 2 sommets (B,H)=(1,-1): [BO']4 ==> Cas2 |
Cas2: Pivoter 4 sommets (B,O)=(-1,-1): [BO']4 |
Remarque : Pour connaitre l'orientation d'un sommet Bas on utilise le truc suivant: On place le triangle:
1. trou = sommet
2. pièce pointe à gauche = +1
3. pièce pointe à droit= -1
 |
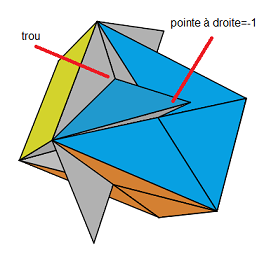 |
| orientation = 1 |
orientation = -1 |
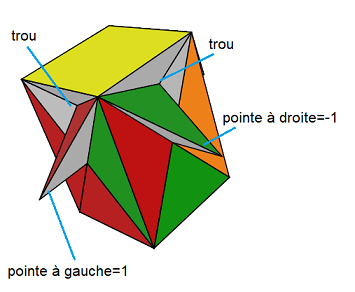 |
|
| pointe gauche=1, droite=-1 |
|
Graphe de sortir
Tout cela suppose qu'on reconnait l'orientation d'un sommet 1 ou -1 mais si on ne sait pas on peut quand même
s'en sortir aveuglement !
posons T = [OH']
4
==> si on a 2 sommets à pivoter on applique T
==> si on a 4 sommets à pivoter on applique F
Le graphe si-dessous vous permet de s'en sortir (aveuglement). Si on a de la chance
on applique seulement F , le pire des cas c'est FTTFF.
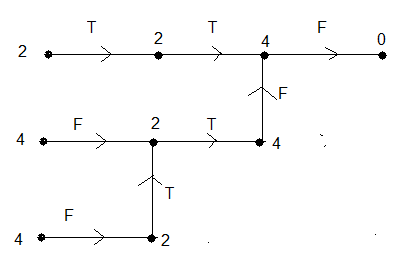 |
|
| Graphe de sortir |
|
F- Formules supplémentaires
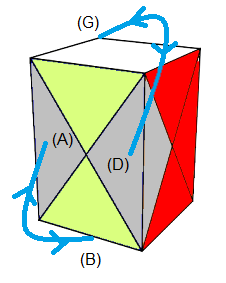 |
 |
| (A)<->(B),(G)<->(D) = [BO'] |
(A)->(G)->(B) = [B'E'][HE] |
1 [2]
Accueil
DMJ: 22/08/2022























