Résolution de la Tour Barrel
20
Sep
2024
Méthode la croix prolongée (Jessica Fridrich)
La tour Barrel est un 3x3x3 tronqué sa résolution se fait exactement comme pour un Rubik's Cube.
Mais comme tous les 3x3x3 modifiés dèsqu' il y a des pièces symétriques on aura des états singuliers.
Notation:
On va nommer les faces :
H(aut) , B(as) , A(vant) , P(ostérieure) , G(auche) , D(roite).
Les rotations
A = tourner 90° la face Avant dans le sens des aiguilles d'une montre.
A' = tourner 90° dans le sens contraire
A² = tourner 180°
 |
|
| Les rotations |
|
A- 1er étage: le Bas
Aucun problème.
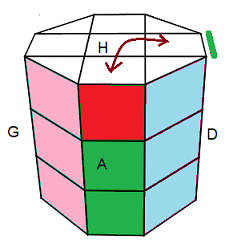
Tenez la tour debout comme indique la fig, et on va choisir le centre blanc comme le Haut.
Puis on place les arrêtes normalement pour faire la Croix. Ensuite les sommets
Attention: Les arêtes doivent correspondre avec les centres latérals ...
 |
|
| La Croix même couleur avec les centres-milieu (centre de l'équateur) |
|
B- 2ème étage: l'équateur
Retournez la tour Haut -> Bas et Bas -> Haut
Pas de prolème non plus pour cette étape. On s'en sort avec les crochets [HD] et [H'A'].
C- 3ème étage: le Haut
Les sommets d'abord
Aucun problèmes. On range donc les sommets avant les arêtes.
Ranger les arêtes
Aucun problème, grâce aux 2 formules:
Glisser 3 arêtes: (HA)->(HP)->(HD) = D².HAP'.D².PA' H.D²
Pivoter 2 arêtes: (HA)°(HD)° = DPGAH .A'HG'P'D' .A'H'AH' (14) (formule propre)
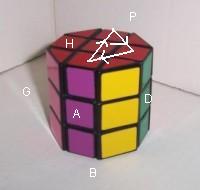 |
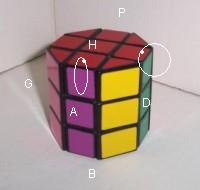 |
| D².HAP'.D².PA'H.D² |
(HA)°(HD)° = DPGAH .A'HG'P'D' .A'H'AH' (14) (formule propre) |
D- Les singularités
A cause de la symétrie de certaines pièces , la tour Barrel gènère 3 singularités.
1. Une seule arête à pivoter.
Il suffit de la pivoter avec une arête-équateur (une couleur) car l'arête-équateur est invariante par pivotement
(HA)° = HGBDA .D'AB'G'H' .D'A'DA' (on pivote aussi (AD))
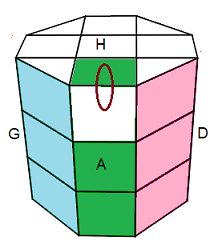 |
|
Une seule arête à pivoter
(HA)° = HGBDA .D'AB'G'H' .D'A'DA' |
|
2. Permuter 2 sommets ou 2 arêtes
Permuter 2 sommets
X =(HDA)<->(HAG) = DBA'HA .B'H'AHG .AG'H'A'D' (15) (en réalité X = (BAD,BGA)(AG,AD))
Posons
Y = G'HD'H² .GH'G'H² .GDH' (13) ; (Y = (HDA,HAG)(HA,HD))
Permuter 2 arêtes : XY ou encore Z = A'H'DH'A .D'HDA'H .D'A'D'AD .H (16)
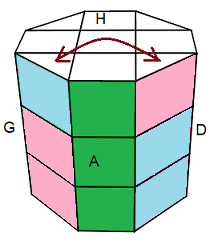 |
 |
| (HDA)↔(HAG)= DBA'HA .B'H'AHG .AG'H'A'D' (15) |
A'H'DH'A .D'HDA'H .D'A'D'AD .H (16) |
1 [2]
Accueil
DMJ: 20/09/2024









