Résolution du Mixup+

Notation:

On va nommer les faces:
H(aut), B(as), A(vant), P(ostérieure), G(auche), D(roite).
h(aut-intérieur), b(as-intérieur), a(vant-intérieur), p(ostérieure-intérieur), g(auche-intérieur), d(roite-intérieur).

Et on fixe le Cube ainsi:
H(aut)=b(lanc), B(as)=j(aune), A(vant)=v(ert), P(ostérieur)=k(lein), G(auche)=o(range), D(roite)=r(ouge)

Les rotations
H = tourner 90° la face Haut dans le sens horaire.
H' = tourner 90° dans le sens contraire
H² = tourner 180°
h = tourner 90° la face hant-intérieur dans le sens horaire (h = H*H').
h₀ = tourner 45° la face hant-intérieur dans le sens horaire.
h'₀ = tourner -45°.

H	h

h0 = 45°

Notation

Le point '.' ou les parenthèses '(', ')' qui se trouvent dans les formules sont là pour faciliter la lecture c'est tout!!!

A- Remettre sous la forme cubique

On veut simplement placer les arêtes-externes pour avoir la forme cubique. Pour ça on se fait aider par 2 fotmules:
- Echanger centre et arête: (A)->{HA} = h'₀ DH'D' h₀
- Pivoter l'arête-externe 45°: {AD}° = h₀ .dHd'. h'₀ H'

Ce qu'on veut

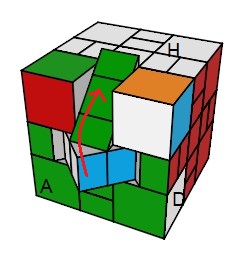(A)->{HA} = h'0 DH'D' h0	{AD}° = h0 .dHd'. h'0 H'

B- Ranger les centres

Tout d'abord il faut connaitre la couleur des faces, si vous ne savez pas, faites vous aider en rangeant les sommets comme dans le POCKET.

Pour nous c'est:
H(aut)=b(lanc), B(as)=j(aune), A(vant)=v(ert), P(ostérieur)=k(lein), G(auche)=o(range), D(roite)=r(ouge)

On place les centres en respectant les couleurs: On échange les centres par:
(A)<->(D) = h₀ A² h'₀ A²

Ce qu'on veut	h0 A² h'0 A²

C- Resoudre le Mixup comme un 3x3x3

On resoud le Mixup comme un 3x3x3 (ignorant les arêtes-internes), la résolution doit se terminer par les arêtes (à la 3étage), là s'il y a une parité c'est une parité sur les arêtes.

Comme un 3x3x3

D- Problème de parité

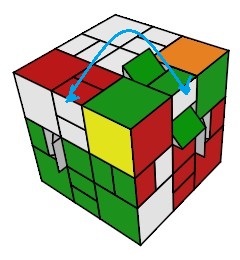
Le Mixup peut gènèrer une parité terrifiante: Permuter 2 arêtes-externes (ou 2 centres c'est pareil)
{HA}<->{HD} = ([AD']h₀ .[D'A]h₀)⁴ [AD']h₀

{HA}<->{HD} = ([AD']h0 .[D'A]h0)4 [AD']h0 Puis résoudre de nouveau le Cube.

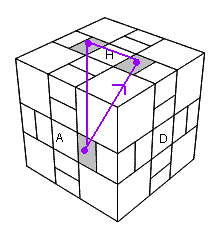
E- Placer les arêtes-internes

On appareille les arêtes-internes avec les arêtes-externes pour former une arête complète. C'est assez simple , mais un peu long.
On ne s'occupe pas des orientations des arêtes-internes (on verra plus tard)

T = h0 G h'0 D' . h0 G' h'0 D

F- Pivoter les arêtes-internes

On pivote les arêtes-internes, C'est la partie la plus longue mais pas bien compliquée.
T = h₀ G h'₀ D' . h₀ G' h'₀ D
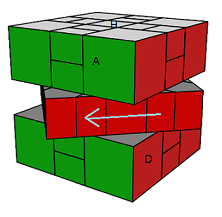
(HG)° (AD)° = TH²TH²

Ce qu'on veut	(HG)° (AD)° = TH²TH²

G- Problème d'orientation

Il y a un problème d'orientation.
Pour ces prolèmes, il n'y a rien à faire il faut apprendre par coeur les formules c'est tout !!!

a0 (Dh')4 H' (hD')4 H a'0

1 [2]

Accueil

DMJ: 24/05/2022