Le 3-Crazy-Mercure
| Difficulté: 20/20 difficile+ |
|
|
7
Dec
3-Crazy-Mercure
Inventeurs: Daqing Bao
Année: 2010
Dim: 57 x 57 x 57mm , 140g
Nombre d'états:
Le 3-Crazy-Mercure est le plus difficile parmi les Crazy-Planètes,
en effet il ne possède qu'une seule rotation normale (1-rotation) ! celà rend les déplacements des pièces extrêmement difficile.
On écrit: Mercure=1
On doit donc déplacer les secteurs à la fin de l'algorithme,
il faut donc avoir des nouvelles formules pour déplacer ces secteurs .
Commentaire
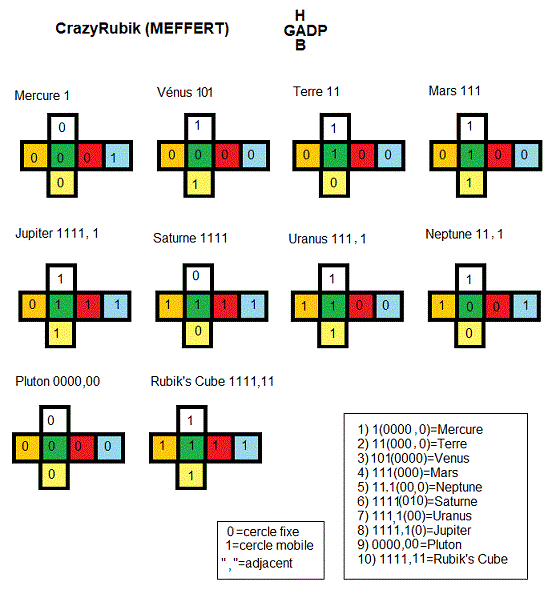
Le codage des planète est bien étrange on dirait un code mathématique mais en faite c'est assez simple et rien de mathématique !! Mais j'ai mis quand
même du temps pour comprendre ce codage !!!
Rien de compliquer les planètes se différent par rapport aux cercles bloqués (face 0 ou 0-face) ou non bloqués (face 1 ou 1-face, normale)
Mercure=1, il a une seule face 1,
Venus=1-1 signifie deux faces 1 opposées (101, séparées par une face 0)
Terre=11 deux faces 1 en série (qui suivent)
Mars=111 trois faces 1 en série
Jupiter=1111+1 cinq faces 1 adjacente, (0, une seule face 0)
Saturne=1111 quatre faces 1 en série, (0-0=010, deux faces 0 opposées , séparées par une face 1)
Uranus=111+1 quatre faces 1 adjacente , (00, deux faces 0 en série)
Neptune=11+1 trois faces 1 adjacentes
Mais Meffert note Neptune=80 !! (pourquoi ?)
Pluton=000000
1- Notation
CONSEIL : Si votre cube a des couleurs différentes alors il vaut mieux convertir les couleurs de votre cube en couleurs des dessins , du genre:
0-blanc (votre cube) ===> 0-klein (dessin)... Pour pouvoir suivre l'algorithme
La première chose à faire c'est qu'il faut chercher les faces à valeur 0,
face 0 ou 0-face = cercle bloqué .
En Crazy les couleurs des faces sont très importantes pour le 3-Crazy-Mercure, on a 5 faces 0 disposées ainsi :
blanc=0, jaune=0, vert=0, klein=1, orange=0, rouge=0.
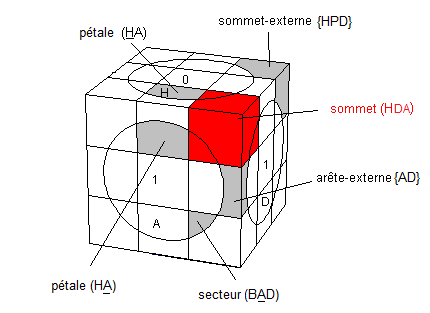
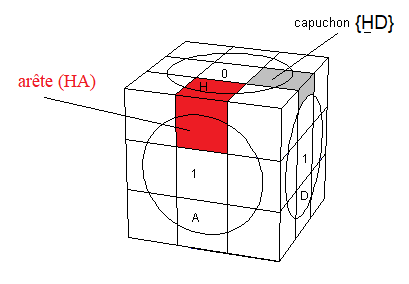
H(aut), B(as), A(vant), P(ostérieure), G(auche), D(roite).
Les rotations
A = tourner 90° la face Avant dans le sens des aiguilles d'une montre.
A' = tourner 90° dans le sens contraire
A² = tourner 180°
d = tourner la tranche d 90°
 |
|
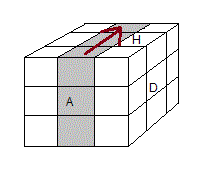| rotation tranche d |
|
Le point '.' et les parenthèses '(', ')' qui se trouvent dans les formules sont là pour faciliter la lecture c'est tout!!!
2- Observation
La particularité de ce puzzle c'est qu'il y a des cercles bloqués qui le rendent redoutable ! .
Même si on arrive à le mettre sous la forme d'un Rubik's Cube normal, il faut quand même le remonter avec seulement 3 rotations en serie ce n'est donc pas évident.
[1] 2
Accueil
DMJ: 16/04/2020
