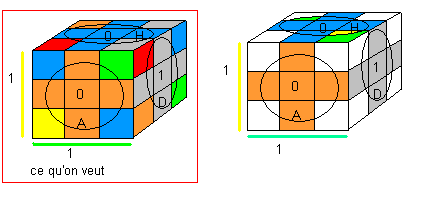
Résolution du CrazyRubik-Mars
1
Aout
2013
Méthode les 6 croix
 Cette méthode divise en plusieurs phases. Le but est d'arriver à un 3x3x3 normal puis le résoudre normalement
Cette méthode divise en plusieurs phases. Le but est d'arriver à un 3x3x3 normal puis le résoudre normalement
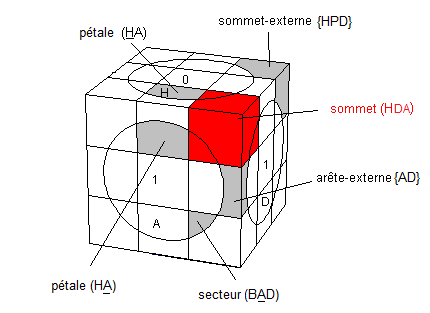
Notation
CONSEIL : Si votre cube a des couleurs différentes alors il vaut mieux convertir les couleurs de votre cube en couleurs des dessins
pour pouvoir suivre l'algorithme .
La première chose à faire c'est qu'il faut chercher les faces à valeur 1,
face 1 ou 1-face = cercle mobile .
Les couleurs des faces du CrazyRubik sont très importantes, pour le CrazyRubik-Mars, on a trois face 1 en série disposées ainsi :
H(aut)=b(lanc)=1 , B(as)=j(aune)=1 , A(vant)=v(ert)=1 , P(ostérieure)=k(lein)=0 , G(auche)=o(range)=0 , D(roite)=r(ouge)=0
Les rotations
A = tourner 90° la face Avant dans le sens des aiguilles d'une montre.
A' = tourner 90° dans le sens contraire
A² = tourner 180°
Le point '.' et les parenthèses '(', ')' qui se trouvent dans les formules sont là pour faciliter la lecture c'est tout!!!
Analyse du puzzle
Avant de lancer dans la résolution, analysons minutieusement ce twist. Le CrazyRubik-Mars, possède 3 cercles bloqués en série, nous disposons donc seulement 3 faces normales qui se suivent.
La difficulté c'est qu'une fois formé le cube normal 3x3x3 il faut le résoudre avec seulement les 3 rotations en serie !!
Phase A: Ranger les arêtes
Les arêtes sont rangées dans un ordres précises !! il faut donc le respecter car au fur et à mesure qu'on avance dans l'algorithme on a peu de place pour travailler !!
A1 :
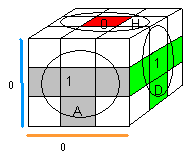
Former la croix de la face Bas=0-orange qui est opposée de la face Haut=0-rouge
Tenez le cube ainsi: H=0-rouge, G=0-klein
On va former successivement les arêtes: (BG), (BP), (BA) et (BD)
La technique d'appareillage: Pour avoir une arête complète.
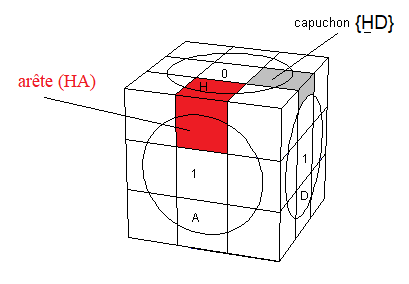
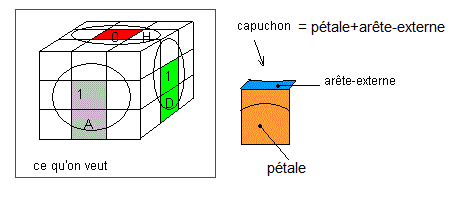
1. On commence par fabriquer le capuchon de avec les deux formules: [H' A' ] et [HD] .
2. Une fois le capuchon est formé (pétale + arête-externe) on appareille avec le pétale pour former l'arête en (AD).
3. On déplace l'arête à son emplacement (on distribue) . Le déplacement est plus ou moins facile celà dépends la composition de l'arête. L'arête (BG) B=0,G=0 est plus dificile à déplacer que l'arête
(BA) B=0 , A=1
Voici les formules pour s'en sortir, il faut veiller que la valeurs des faces soient toujours correctes, par exp: H=0, A=1, D=1 ....
- On forme le capuchon avec: [H' A' ] ou [HD]
- Echanger 2 capuchons : {HA}<->{HD}: H. DHD'.H.DH²D'
- Permuter 3 capuchons: {HD}->{HP}->{HG}: DHD'.H.DH²D'
- {HP}->{HA}->{HD}: A[DH]A'
- Pour pivoter l'arête-externe : {HA}° = [H' A' ][HD]
- Pour séparer arête-ex et pétale : [D' A]A'
 |
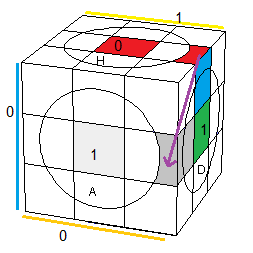 |
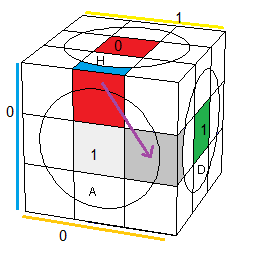
| (HA)->(AD) = [H'A'] |
(HD)->(AD) = [HD] |
Ranger (BG)
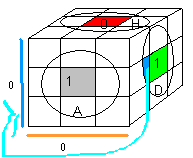
Fabrication l'arête (BG): Dans le cas (BG) B=0,G=0 , on déplace séparament les deux parties :
le pétale puis le capuchon
 |
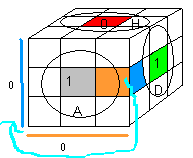 |
| (AD)->(BG) = D' B² |
{AD}->{BG} = A² G |
Ranger (BP), (BA), (BD)
Une fois l'arête formée en (AD) on la déplace à son emplacement.
On fait la même chose avec (BA) et (BD).
Veillez que les couleurs des arêtes correspondent bien comme indiqueent les dessins
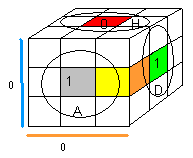 |
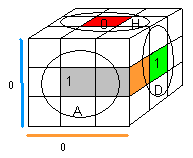 |
| (AD)->(BP) = D²P' |
(AD)->(BA) = A |
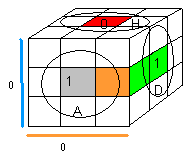 |
|
| (AD)->(BD) = D' |
|
A2 :
Finir l'équateur
Utiliser la même stratégie pour finir l'équateur, aucun problème.
A3 :
Former la dernière croix la face 0-rouge
Cette partie est la plus pénible de tout !! On sert la zone (AD) comme zone de travail, pour fabriquer les capuchons.
On forme d'abord le "+" du cercle rouge, puis les capuchons (à tête rouge) puis la croix.
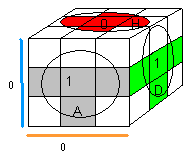 |
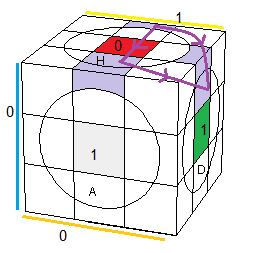 |
|
A[DH]A' |
A4 :
Parité: permuter deux arêtes-externes
Parfois on tombe sur cette redoutable parité:
Deux arêtes-externes à échanger: {HA} <-> {HD}.
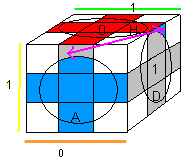 |
|
| Parité: {HA} <-> {HD} |
|
Ma statégie est simple .
1. Echanger d'adord les 2 pétales: (H
A)->(H
D)->(A
D) = [HA] H'DH [AH]D'
2. Permuter 2 capuchons : {H
A}<->{H
D} = H' .DH²D'H .DHD'H²
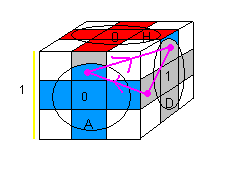 |
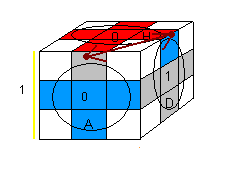 |
| 1. [HA] H'DH [AH]D' |
2. H' .DH²D'H .DHD'H² |
Formules supplémentaires
Voici 2 formules intéressantes:
 |
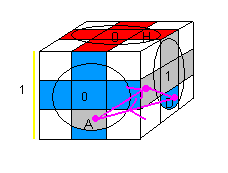 |
| [HA] H'DH [AH]D' |
D'[B'A']BDB'[A'B'] |
Phase B: Former des sommets
Placez le cube en position : D=1-blanc et B=1-vert
Cette phase est bien plus agréable que la précédante, mais un peu plus longue, car il y 24 secteurs à appareiller pour former les 8 sommets.
Il faut quand même faire attention, de ne pas se tromper entre les 0-rotations et les 1-rotations (rotations normales) !!
On place le cube comme indique la fig: D=1-blanc et B=1-vert . Durant le travail veillez que la croix Haut (klein) soit toujours correct.
Utiliser : [D' B' ] pour monter le sommet (BAD): (BAD)->(HDA)= [D' B' ]
ou [GB] pour monter le sommet (BGA): (BGA)->(HAG)= [GB]
puis H, H', H² pour fusionner un secteur avec un sommet-externe ...
N'oubliez pas qu'on monte ou descend un sommet que par les 1-faces.
[D'B'] : D->H
[D'B']
3 : B->H
[B'D'] : A->H
[D'B']² : pivoter -90°
Phase C: Résoudre le cube comme un 3x3x3
C'est pratiquement fini maintanant. Le coeur de cette partie c'est qu'il faut trouver des formules utilisant seulement trois rotations en serie, aucun probème, les voici:
Trois formules magiques
T = [HA]P' [AH]P : déplacer 3 sommets (A,H,P ===> 3 rotations en série)
V = DHD'.H.DH²D'.H² : pivoter 3 sommets
E = D²H' D' H'.(DH)².DH' D : glisser 3 arêtes
C1 :
Finir la face 0-klein
Tenez le cube: D=1-blanc et B=1-vert
=> Rendre le Haut tout klein
=> Touner H pour bien ranger les arêtes-Haut
=> Reranger les sommets-Haut si nécessaire
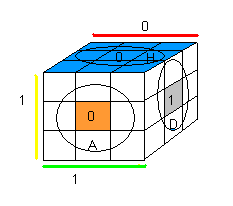 |
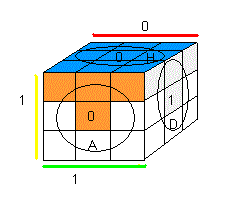 |
| Descendre/Monter un sommet par 1-face |
Descendre/Monter/pivoter un sommet par 1-face |
C2 :
Finir l'équateur
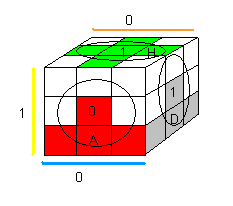
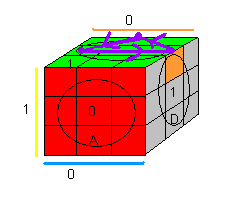
Retournez le cube: D=1-blanc , H=1-vert . Tenez le cube comme indique la figure ci-dessous, on finit l'équateur en utilisant :
E = (HG)->(HD)->(HP) = D²H' D' H'.(DH)².DH' D et la conjugaison
 |
 |
|
(HG)->(HD)->(HP) = D²H' D' H'.(DH)².DH' D |
C3 :
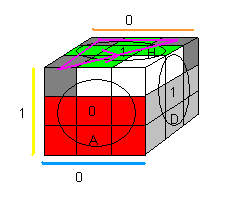
Placer les sommets
on place les sommets avec: [HD] .G'[DH]G
 |
|
| (HGP)->(HAG)->(HPD) = [HD] .G'[DH]G |
|
C4 :
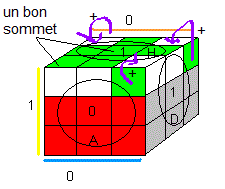
Orienter les sommets
Tenez le cube en D=1-blanc et H=1-vert : On oriente les sommets avec: V
on commence par avoir un seul sommet "bon" sur le Haut, puis on pivote les 3 autres restant
 |
|
| V = DHD'.H.DH²D'.H² |
|
C5 :
Finalement glisser les 3 arêtes
Tenez le cube en D=1-blanc et H=1-vert
 |
 |
| E = D²H' D' H'.(DH)².DH' D |
Et voilà !!! |
1 [2]
Accueil
DMJ: 20/11/2022
 Cette méthode divise en plusieurs phases. Le but est d'arriver à un 3x3x3 normal puis le résoudre normalement
Cette méthode divise en plusieurs phases. Le but est d'arriver à un 3x3x3 normal puis le résoudre normalement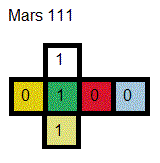
 Cette méthode divise en plusieurs phases. Le but est d'arriver à un 3x3x3 normal puis le résoudre normalement
Cette méthode divise en plusieurs phases. Le but est d'arriver à un 3x3x3 normal puis le résoudre normalement