Solution du Crazy Domino+
6
Nov
2010
Le Crazy Domino+
Le Crazy Domino+ est un Mod du Crazy Domino, il est passionnant, la plupart du temps les rotations contenant les cercles sont bloquées! on dispose alors seulement 4 rotations . La résolution est donc plus difficile.
Notation
On va nommer les faces et les couleurs ainsi:
H(aut)=b(lanc) , B(as)=j(aune) , A(vant)=v(ert) , P(ostérieure)=k(lein) , G(auche)=o(range) , D(roite)=r(ouge)
d(droite-intérieur), a(avant-intérieur) .
Les rotations
A = tourner 90° la face Avant dans le sens des aiguilles d'une montre.
A' = tourner 90° dans le sens contraire
A² = tourner 180°
d = tourner 90°
D² se lit slash (/)

2-Crazy+
A- Finir les cercles
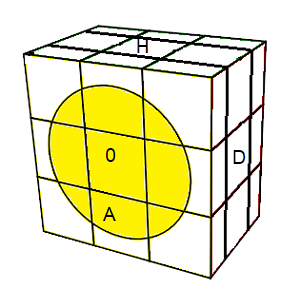
Tenez le cube comme indique la fig ci-dessous: La face A=cercle et P=cercle, les faces A et P considèrées comme bloquées,
on disposse alors seulement 4 rotations: G,D,H,B
 |
|
| A=cercle-jaune, P=cercle-blanc |
|
A1:
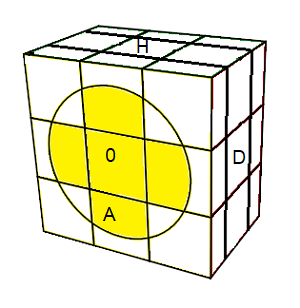
Finir les deux Plus "+" des cercles
On place des pétales "couché", c'est intutif et c'est facile.
 |
|
| Le "+" |
|
A2:
Former les cercles
On place les secteurs avec la couleur du centre pour former les cercles.
Pour ça il suffit de placer les sommets puis les pivoter si nécessaire.
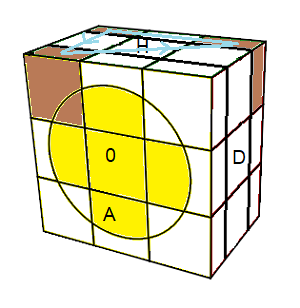
placer: (HGP)->(HAG)->(HPD) = [DH] .G'[HD]G
pivoter:(HGP)
-(HAG)
+ = [DH]² .G'[HD]²G
 |
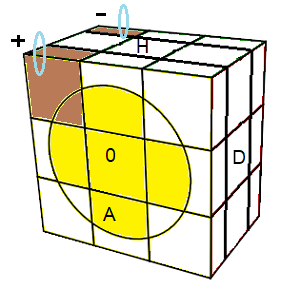 |
| (HGP)->(HAG)->(HPD) = [DH] .G'[HD]G |
(HGP)-(HAG)+ = [DH]² .G'[HD]²G
|
B- Ranger les sommets-externe-Bas
On arrive maintenant à un Crazy Domino normal (ignorez l'équateur), ça se résoud normalement comme un Crazy Domino.
Tenez le cube comme indique la fig ci-dessous
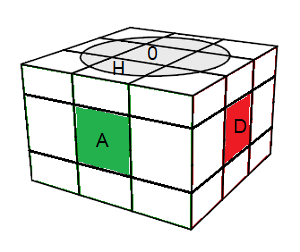 |
|
| cercle-blanc = Haut |
|
Trouvez le sommet-ex Bas correspondant (grâce à ses 3 couleurs)
Rangez un sommet-ex Bas (on descend les sommets-ext Bas):
{HDA}->{BAD}: I = (D²H)² . (D²H²)²
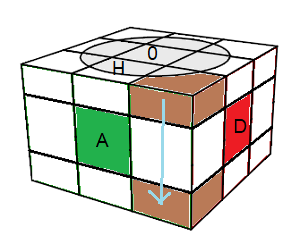 |
|
{HDA}->{BAD}: I = (D²H)² . (D²H²)²
|
|
C- Ranger les sommets-externe-Haut
Acrochez vous, car la formule est assez longue !!
Voici la formule magique !!!
V = D²HD²H '. D²A²H ' A² . (D²H²)
3 . BD² . (D²H²)
3 B'
V permute {HDA}<->{HPD}
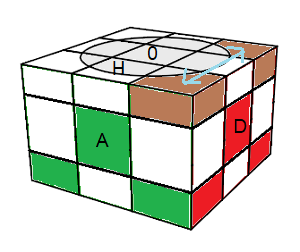 |
|
| {HDA}<->{HPD} = D²HD²H '. D²A²H ' A² . (D²H²)3 . BD² . (D²H²)3 B' |
|
D- Ranger les arêtes-Bas
Cette partie est plus simple que la précedente
I = (D²H)² . (D²H²)²
I² déplace 3 capuchons-Haut: {H
P}->{H
A}->{H
D} !!
N = (Hd²)²H² descend 2 capuchon-opposé : {H
A}->{B
A} et {H
P}->{B
P}
Avec I² et N on peut ranger toutes les arêtes du Bas
Note : Si besoin, on peut utiliser les rotations a² ou d² pour monter les arêtes , les positionner (toujours en opposé) avec I² , puis les redescendre avec N.
On ne touche pas les sommets, car les rotations a², d² ne les touchent pas
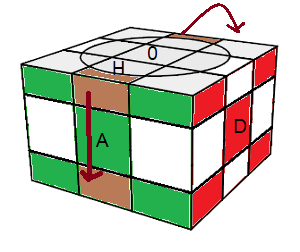 |
|
| N = (Hd²)²H² |
|
E- Ranger les arêtes-Haut
C'est prèsque fini .... deux formules au choix:
I = (D²H)² . (D²H²)²
I², déjà vu : I² déplace 3 capuchons-Haut: {H
P}->{H
A}->{H
D}
Q = D²HD²H'(D²H²)² .D²H' D²H(D²H²)² déplace 3 capuchons-Haut: {H
P}->{H
A}->{H
D}
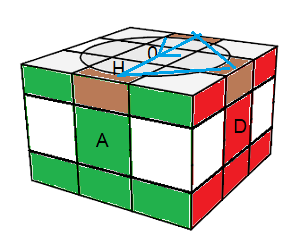 |
 |
I²
avec I = (D²H)² . (D²H²)² |
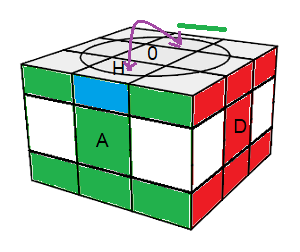
état singulier (1) : d (D²H²)² d ' .D²H² |
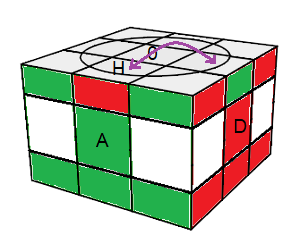 |
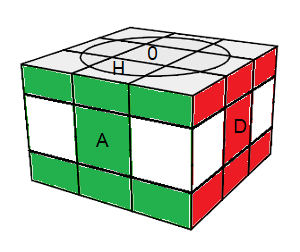 |
| état singulier (2) : I² revient à l'état singulier (1) |
Et voilà, il nous reste l'équateur à finir |
F- Finir l'équateur
Aucun problème, avec E = D²H'D'H' .(DH)² .DH'D = (HG)->(HD)->(HP) on peut déplacer 3 arêtes de l'équateur.
(BD)->(HG)->(HD) = ED²E' D²
Tenez le cube comme indique la fig ci-dessous
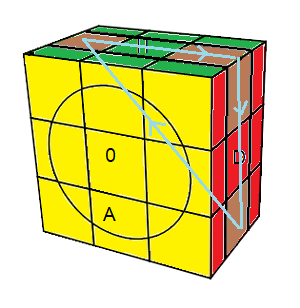 |
 |
(BD)->(HG)->(HD) = ED²E' D²
avec E = D²H'D'H' .(DH)² .DH'D |
Et hup laaaaaa!!! |
1 [2]
Accueil
DMJ: 11/08/2022

















