Résolution du Crazy Domino
11
Aug
2022
Par morphocode
Le Crazy Domino est un merveilleux cube, il est extêmement passionnant, j'avoue que j'ai beaucoups de mal pour m'en sortir! Il faut dire que parmi les 8 sommets il y en a un qui bloque le cercle,
c'est ce qui le rend passonnant et "crazy" !!!
J'ai mis plusieurs jours pour trouver un algorithme de résolution, la résolution se fait par plusieurs phases, accrochez-vous !!!!!
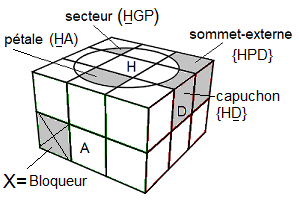
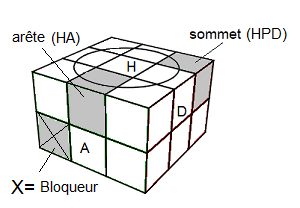
Notation
On va nommer les faces et les couleurs ainsi:
H(aut)=b(lanc) , B(as)=j(aune) , A(vant)=v(vert) , P(ostérieure)=k(lein) , G(auche)=o(range) , D(roite)=r(ouge)
d(droite-intérieur), a(avant-intérieur) .
Les rotations
A = tourner 90° la face Avant dans le sens des aiguilles d'une montre.
A' = tourner 90° dans le sens contraire
A² = tourner 180°
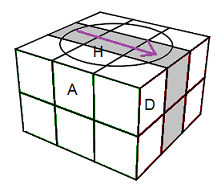
d = tourner 90°
D² se lit slash (/)
 |
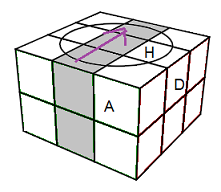 |
| Rotation a |
Rotation d |
A- Finir les cercles
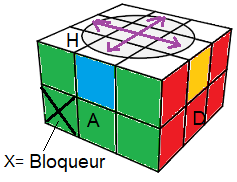
La première chose a faire c'est détecter le sommet qui bloque les cercles nous l'appelons le
Bloqueur.
Pour le trouver il suffit de monter un sommet et voir si le cercle-Haut est bloqué, si oui dans ce cas ce sommet est le Bloqueur.Une fois trouvé , placez le en (BGA).
Tous les formules se référent à ce Bloqueur, il doit être en bonne position sinon ça détruira tout le cube!. C'est pourquoi avant d'appliquer une formule
il faut avoir le réflexe de se demander "est ce que le Bloqueur est en bonne position pour cette formule ?".
Sur mon cube le Bloqueur = jaune-orange-vert.
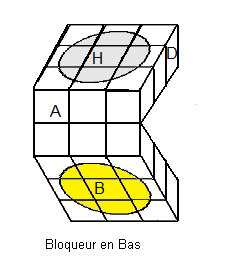
On prend le Haut=blanc (centre blanc), Bas=jaune (centre jaune)
 |
|
| Ce qu'on veut |
|
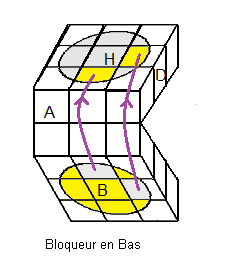
Former le "+" blanc
On commence par former le "+" du cercle Haut, càd placer les 4 pétales Haut (blanc) , c'est facile
|
 |
|
(A²D²)3 |
 |
 |
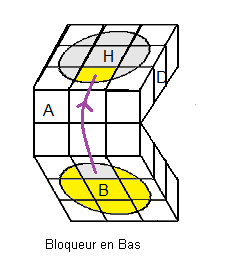
| D²A²D² |
dH²d' .D²A² |
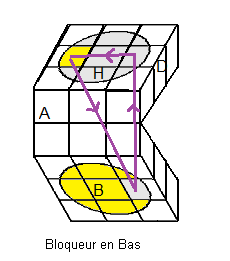
Former le cercle blanc
On place les 4 secteurs Haut (blanc).
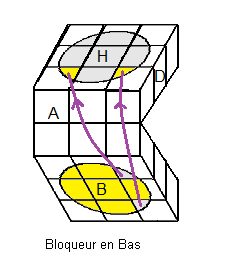 |
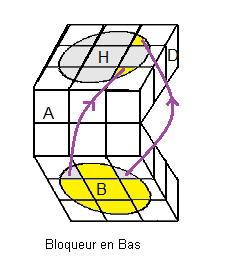 |
| (D²A²)2 |
(A²D²)2 |
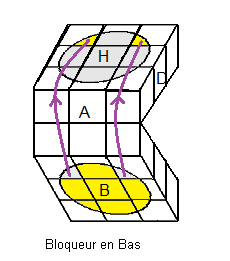 |
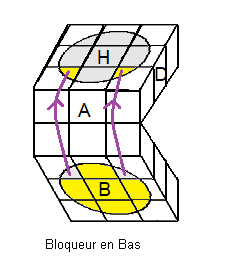 |
| dH²d' .A² |
(A²D²)4 |
Rappel : d=90° , d²=180° , D=90° et D²=180° (se lit slash=/)
B- Placer des sommets-Bas
Positionnez le Bloqueur en (BGA)
Voici 3 merveilleuses formules !! à conserver précieusement dans votre poche !!, ce qui est merveilleux c'est que ces formules ne touchent pas le cercle!!!
Bloqueur = (BGA)
I = (D²H)² . (D²H²)²
J = (D²H')² . (D²H²)²
K = (P²H')² . (P²H²)²
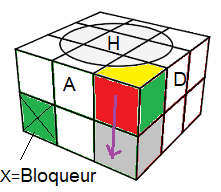
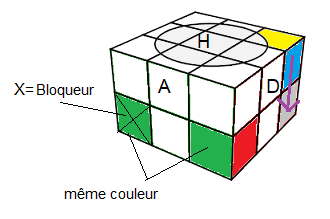
On place les sommets Bas en basant sur les couleurs du Bloqueur :
(BAD) avec A=vert, B=jaune
(BDP) avec D=rouge, B=jaune
(BPG) avec P=klein, B=jaune
Comme dans le Pocket
 |
 |
| I = (D²H)² . (D²H²)² |
J = (D²H')² . (D²H²)² |
 |
|
| K = (P²H')² . (P²H²)² |
|
C- Ranger les sommets-Haut
Acrochez vous !!! c'est ici qu'il faut s'accrocher !!!
Voici la formule magique, que j'ai tant souffert pour la trouver !!!
Bloqueur = (BPG)
V = (HDA)<->(HPD) = D²HD²H' .D²A²H'A² .(D²H²)
3 .BD² .(D²H²)
3 !!!! (1er découverte)
 |
|
Bloqueur = (BPG)
V : (HDA)<->(HPD) |
|
D- Ranger les arêtes-Bas
Cette partie est plus simple que la précedente
Grande découverte:
I² déplace 3 capuchons: {H
P}->{H
A}->{H
D} !!(2ème découvert)
(Hd²)²H descend 2 capuchons-opposé : {H
A}->{B
A} et {H
P}->{B
P}
Alors si on pose N = (Hd²)²H
Avec I² et N on peut ranger toutes les arêtes du Bas
Note : Si besoin, on peut utiliser les rotations a² ou d² pour monter les arêtes , les positionner (toujours en opposé) avec I² , puis les redescendre avec N.
On ne touche pas les sommets, car les rotations a², d² ne les touchent pas.
 |
|
{HA}->{BA} et {HP}->{BP}
= (Hd²)²H |
|
E- Ranger les arêtes-Haut
C'est fini, on arrive à la fin ..... deux formules pour s'en sortir, déjà vu : I²
I² déplace 3 capuchons: {H
P}->{H
A}->{H
D} !!(2ème découvert)
et d (D²H²)² d ' .D²H² permute 2 capuchons
NOTE : On regarde les arêtes par rapport aux couleurs des
sommets-Haut
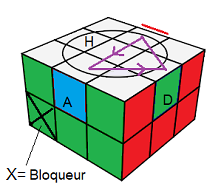 |
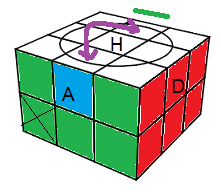 |
| I² |
état (1) : d (D²H²)² d ' .D²H² |
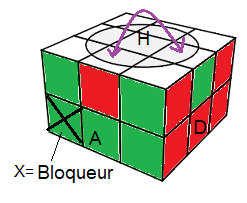 |
 |
| état (2) : I² revient à l'état (1) |
Et hupp laaaa!!!!! |
REMARQUE IMPORTANTE : Pour les états (1) et (2), certains Cubeurs (dans les tutos en vidéo de Youtube,ou dans les forums ...) disent qu'on a là un "problème de parité" . C'est complétement FAUX !!!
En effet le Crazy Domino n'a pas de loi de parité comme le Rubik's Cube. Les arêtes et les sommets ne sont pas forcement en phase . Si les sommets
a une permutation paire, les arêtes peuvent avoir une permutation impaire (voir la rotation D² par ex) , donc les états (1) et (2) sont des états légitimes du cube !! on n'a violé aucune loi ... donc ce ne sont pas
des problémes de parité !
Souvent ils utilisent l'expression "problème de parité" n'importe comment, car ils ne comprennent pas réellement cette expression, ===> Méfiez vous !!!
Et n'oubliez pas le
SLOGAN:
Sur le net, n'importe qui peut dire n'importe quoi, et n'importe quoi peut être répété bêtement par n'importe qui !!
Nous dirons que les états (1) et (2) sont des états singuliers, un état singulier est un état légitime qu'on s'en sort difficilement .
F- Formules suplémentaires
Voici quelles que formules suplémentaires.
 |
 |
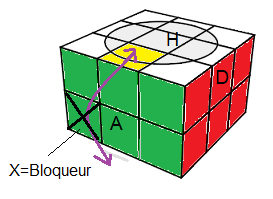
(d²H²)² .H (d²H²)² H' ou bien
(Hd²)6H² |
D²HD²H'(D²H²)² .D²H'D²H(D²H²)² |
 |
|
| D²A²D² |
|
1 [2]
Accueil
DMJ: 11/08/2022