Bienvenue sur Fan2Cube ...
LES ROTATIONS
 - Si vous ne connaissez pas encore le Rubik's Cube, alors vite procurez-en vous un ! car c'est un objet merveilleux, plein de science et de mystère,
un casse-tête redoutable.
- Si vous ne connaissez pas encore le Rubik's Cube, alors vite procurez-en vous un ! car c'est un objet merveilleux, plein de science et de mystère,
un casse-tête redoutable.
Vous pouvez acheter le Rubik's Cube dans:
- La Grande Récré
- Nature Découverte
- Amazon.fr
- La Fnac
Les Cubes à avoir....
 4 Cubes qu'on doit avoir dans sa collection:
4 Cubes qu'on doit avoir dans sa collection:
* Le Mirror Block
* Le Void Cube
* Le Skewb
* Le Square-1
 La production en masse de Golden Cube (2017) par FANGCUN
La production en masse de Golden Cube (2017) par FANGCUN
 Un événement s'est produit en 2017 totalement inaperçu : La production en masse du Golden Cube de Tony FISHER !!
Un événement s'est produit en 2017 totalement inaperçu : La production en masse du Golden Cube de Tony FISHER !!
Le Golden Cube est né en 1999, l'oeuvre de Tony FISHER, il introduit plusieurs concepts innovants :
1) D'abord le design, dissymétrique, vraiment joli ça invoque le côté chic
2) La position START : La résolution se fait à partir de cette position
3) Le concept 'homotopie' : Les couleurs sont remplacées par des formes ! toutes les pièces ont une forme différente,
ça rend vraiment difficile à reconnaitre une pièce, alors que avec les couleurs c'est assez facile.
4) Le concept 'singularité' . Une singularité est un état où l'on a l'impression de violer une loi du Cube.
Le Skewb a une loi sur les sommets , rappelons brèvement cette loi (la loi des twists):
Quand les sommets sont "isolés" (les sommets haut sont en Haut, les sommets bas sont en Bas) alors on a:
- Soit on pivote 2 sommets dans les sens opposés
- Soit on pivote 3 sommets dans le même sens
Quand les sommets sont isolés, le Golden Cube peut avoir un état où l'on doit pivoter un seul sommet s ! on nomme cet état :
la singularité-sommet. On a donc l'impression de violer la loi des twists, mais en réalité on n'a pas violé la loi, on a bien pivoté deux
sommets 120° et -120° , on a pivoté le sommet s avec le sommet Triangle équilatéral , comme ce triangle
est invariant par pivotement , on voit seulement le sommet s pivoté !!
 En 2007 MEFFERT produisait le Golden Cube en masse mais il était beaucoup plus gros (81mm centre 57mm) et perdait
la possibilité de générer la singularité-sommet, puisque le Triangle-équilatéral n'était plus équilatéral !!!! c'est vraiment dommage !!
Le Golden Cube de MEFFERT est donc un faux Golden Cube!! c'est simplement un SuperSkewb ou un Skewb Ultimate !
En 2007 MEFFERT produisait le Golden Cube en masse mais il était beaucoup plus gros (81mm centre 57mm) et perdait
la possibilité de générer la singularité-sommet, puisque le Triangle-équilatéral n'était plus équilatéral !!!! c'est vraiment dommage !!
Le Golden Cube de MEFFERT est donc un faux Golden Cube!! c'est simplement un SuperSkewb ou un Skewb Ultimate !
Ce qui est vraiment dommage car le Triangle-équilatéral était prèsque équilatéral !.
En 2017 FANGCUN reproduisait en masse le Golden Cube, cette fois-ci FANGCUN a bien réussi !! le Golden Cube de FANGCUN génère la singularité-sommet
bravo FANGCUN. Il fallait attendre 18 ans !!
Pour des raisons inconnues le Cube était rebaptisé "Ghost Skewb" !!
ce qui fait que sa sortie est totalement inaperçu !
C'est un Cube de très bonne qualité à prix raisonnable.
il mesure 61mm (contre 57mm) bravo FANGCUN ....
Il faut absolument ce Golden Cube (Ghost Skewb) de FANGCUN quoiqu'il en coûte !
 Le Golden Cube II de Tony (2014)
Le Golden Cube II de Tony (2014)
 Un événement s'est passé totalement inaperçu: Le Golden Cube II !! En effet Tony a réalisé (2014) la version II de son Golden Cube, dans cette nouvelle version on a un nouveau design aussi joli que la version précédente mais on a en plus
la possibilité d'avoir des singularités ...
Un événement s'est passé totalement inaperçu: Le Golden Cube II !! En effet Tony a réalisé (2014) la version II de son Golden Cube, dans cette nouvelle version on a un nouveau design aussi joli que la version précédente mais on a en plus
la possibilité d'avoir des singularités ...
En 2014, Tony travaille de nouveau sur le Golden Cube, cette fois-ci c'est vraiemnt le top du top !!! le Golden Cube II, non seulement il est joli, chic mais il peut générer 2 singularités:
une singularité-sommet et une singularité-centre !! c'est vraiment le maximum qu'un Skewb peut nous offrir , bravo Tony ...
On souhaite vivement sa production en masse comme le fait HKnowstore pour le Ball-in-cube et l'Overlapping.
Il y a aussi une version bandage de Golden Cube II, (ces Cubes coutaient quand même 200£ sur le site de Tony!!) .
 Le Golden Dodécaèdre
Le Golden Dodécaèdre
 En 2018 Tony a réalisé ce Cube en version 2,7cm et l'a présenté dans le Dutch Cube Day 2018, c'est la même chose que le Golden Cube mais en forme dodécaèdre, come le Golden Cube origine il a
une pièce symétrique (le triangle équilatéral) qui lui permet de générer une singularité.
En 2018 Tony a réalisé ce Cube en version 2,7cm et l'a présenté dans le Dutch Cube Day 2018, c'est la même chose que le Golden Cube mais en forme dodécaèdre, come le Golden Cube origine il a
une pièce symétrique (le triangle équilatéral) qui lui permet de générer une singularité.
C'est un joli twist, son design, dissymétrique rend vraiment difficile à reconnaitre les pièces ... Il faut connaitre par coeur la forme des pièces et leur emplacement avant de le mélanger !!!
!!
En 2019 MEFFERT produit en masse ce Golden Dodécaèdre, mais manque de pot le triangle n'est pas invariant par pivotement (contairement avec la version origine) !
du coup pas de singularité ! lorsqu'on pivote ce sommet, la pièce pointe légèrement vers le haut ! au lieu de rester plat, c'est vraiment, vraiment dommage !!!
Ce qui est vraiment dommage car ce triangle est prèsque équilatéral
La version du Golden Dodécaèdre de MEFFERT est plus gros 8cm (comme le Skewb Ultimate). C'est une production de très bonne qualité je vous conseille donc d'en avoir un dans votre collection qui remplacera
le Golden Cube.
Bravo Tony ...
Maintenant , il faut absolument négocier, convaincre ... MEFFERT, HKNOWSTORE, ... pour qu'ils reproduisent en masse le Golden Cube II, le Golden Cube II bandage ....
NOTE :
¤ Mirror = les pièces gardant la même forme mais ont les dimensions différentes.
*Mirror block = Mirror Rubik's Cube
*Mirror Pocket
*Mirror Skewb
*Mirror Square-1
...
¤ Ghost = toutes les pièces ont une forme différente.
*Ghost Cube
*Ghost Pocket
*Ghost Pyraminx
*Golden Cube = Ghost Skewb
*Golden Dodécaèdre = Ghost Skewb Ultimate
...
Simple mais efficace ...
Avec seulement 2 formules pour restaurer le Domino!
- Placer les arêtes: (HA)->(HP) = (H²D)3
- Placer les sommets: (BGA)->(BAD)->(HGP) = HDH' .G(HDH')G
 |
 |
| (HA)->(HP) = (H²D)3 | (BGA)->(BAD)->(HGP) = HDH' .G(HDH')G |
Belle découverte ...
Il est vraiment remarquable qu'on peut résoudre le Skewb avec seulement une seule formule [DG'] !!
¤ Se mettre en position START (isoler les sommets)
Les 4 sommets blancs en Haut
- Placer les sommets Haut: (HDA)<->(HGP) = [DG']
- Placer les centres: (H)->(D)->(A) = [DG']²
- Orienter les sommets: (BGA)-(BDP)+ = [DG']3 tH² [DG']3
 |
 |
| Position START | (HDA)<->(HGP) = [DG'] |
 |
 |
| (H)->(D)->(A) = [DG']² | (BGA)-(BDP)+ = [DG']3 tH² [DG']3 tH² |
NOTE tH² signifie tournez le cube suivant H² (tournez le cube entier 180° suivant la face (H))
[DG']3 tH² [DG']3 tH² = [DG']3[GD']3
L'algorithme minimal
Il est vraiment remarquable qu'on peut restaurer le Rubik's Cube avec une seule formule J !! :
on poseDe plus la formule est structurée, construite autour du commutateur [DH] donc facile à retenir et à comprendre ce que fait la formule.
ABA' = BA
J = A[DH]A'.H
J = [DH]AH
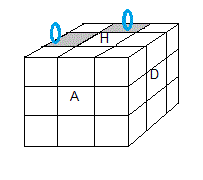
- Placer les arêtes: (HG)<->(HP) = J
- Placer les sommets: (HGP)<->(HDA) = J (en veillant de ne pas toucher (HG) et (HP))
- Orienter les arêtes: (HG)+(HP)+ = J²
- Orienter les sommets: (HGP)+(HAG)+(HDA)+ = J4
 |
 |
| (HG)<->(HP) = A[DH]A'.H | (HGP)<->(HDA) = A[DH]A'.H en veillant de ne pas toucher (HG) et (HP) |
 |
 |
| (HG)°(HP)° = (A[DH]A'.H)² | (HGP)+(HAG)+(HDA)+ = (A[DH]A'.H)4 |
Voici un petit livret de solution du Rubik's Cube sous la forme d'image .gif vous pouvez donc le telécharger imprimer, couper et agraffer pour faire un petit livret.
Il n'y a aucune raison que vous n'arrivez pas !!! ...
.::Solution en VIDEO pour les allergiques aux formules::.
Super Mégaminx
- Si votre Mégaminx a des centres orientés, voici 2 formules pour s'en sortir. Pivoter les centres:
 |
 |
| (A)+ = (H'² D²H².AD'²A)3 | (A)- = (D²H'² D'².A' H²A')3 |
- Voici mon Super Mégaminx (avec les centres orientés), c'est assez joli quand on le mélange
 |
 |
| Mélangé | Et voila ... |
Le diamètre du twist c'est la distance maximale entre deux états.
En Août 2014 Tomas Rokicki et Morley Davidson démontrent que le diamètre du Rubik's Cube est 26 (33 ans de galère !!!)
On se demande donc quels sont des états (les plus loin) qui demandent 26 rotations pour atteindre ? Michael Reid (1998) a trouvé cette formule par ordinateur
∏ = H²B²G A²H'BD²PH'B'DGA²DHB'D'GHA'P'
et a prouvé que c'est une des plus courte formule |∏| = 26
cet état est nommé le SuperFlip4Spot, c'est donc l'un des états les plus loin du Cube.
Pourquoi on l'appelle SuperFlip4Spot parce qu'on a: ∏ = Φ Ω = Ω Φ
On ne connait pas beaucoup des états de longueur 26, à part ce SuperFlip4Spot !!
* Le SuperFlip (12 arêtes retournées)
Φ = D'H²PG'AH'PBAHB'GB²A'DP'BA'H'P'HB'
Michael Reid a trouvé cette formule en 1995 par ordinateur et c'est Jerry Bryan qui démontre (1995) que c'est la plus courte formule |Φ| = 24
Le SuperFlip joue un rôle important, il est le seul (à part l'identité e) dans le centre de G (le groupe du Rubik's Cube).
*4Spot face(A,P) et face(G,D) = Ω = BP²A²BH'G²D²H' (12*)
Les Nouveautés du mois
 Bravo MEFFERT pour la production en masse de Golden Ultimate (Golden Dodecahedron) de Tony... il est vraiment super, très très bonne idée.
La version du production est plus gros (8cm) que la version d'origine (2,7cm) mais elle possède quand même le triangle équilatéral ce qui est essentiel . Le design est joli, c'est un puzzle de collection il faut absolument en avoir un dans sa collection.
Bravo MEFFERT pour la production en masse de Golden Ultimate (Golden Dodecahedron) de Tony... il est vraiment super, très très bonne idée.
La version du production est plus gros (8cm) que la version d'origine (2,7cm) mais elle possède quand même le triangle équilatéral ce qui est essentiel . Le design est joli, c'est un puzzle de collection il faut absolument en avoir un dans sa collection.
Bravo MEFFERT !! Il vous reste maintenant de produire en masse d'autres cubes comme: le Golden Cube II, le Golden Cube II bandage ,....
Ghost Cube
 Super bonne nouvelle : Le Ghost Cube est sorti en masse !!!, ça fait des années qu'on réclame sa sortie houf! enfin il est là. Un super design, aussi beau et chic que le Golden Cube !!! .
Le Ghost Cube est un 3x3x3 mais chaque pièce est différente, pour le restaurer il faut connaitre parfaitement les pièces et leur orientation comme le Golden Cube. Si le Golden Cube est le Roi des Skewb alors le Ghost Cube est le Roi des Rubik.
La version métalisée (Or, Argent, Vert, ...) est 20 fois plus joli que la version stickers !! et puis on n'a plus peu de perdre les minuscules étiquettes.
Super bonne nouvelle : Le Ghost Cube est sorti en masse !!!, ça fait des années qu'on réclame sa sortie houf! enfin il est là. Un super design, aussi beau et chic que le Golden Cube !!! .
Le Ghost Cube est un 3x3x3 mais chaque pièce est différente, pour le restaurer il faut connaitre parfaitement les pièces et leur orientation comme le Golden Cube. Si le Golden Cube est le Roi des Skewb alors le Ghost Cube est le Roi des Rubik.
La version métalisée (Or, Argent, Vert, ...) est 20 fois plus joli que la version stickers !! et puis on n'a plus peu de perdre les minuscules étiquettes.
Mais il y a un petit hit !!! la production de masse comporte des défauts de fabrications (trop d'espace entre les coupes!) ça gaspille un peu le twist. Il fallait augmenter la
dimension 60x60x60mm par exemple (au lieu de 57x57x57mm) pour avoir les coupes fines et nettes !!, il vaut mieux avoir un cube un peu plus gros
mais parfait que d'avoir un cube petit mais plein de défaut !!!
Ghost Cube= , production=
, production=
 Overlapping
Overlapping

 J'aime beaucoup ce twist, bien que le design est un peu différent que celui d'origine mais il est néanmois joli. C'est un puzzle de très bonne qualité
mais reste fragine, il faut le manipuler avec douceur . La version origine de Tony daté en 2004 , le design est légèrement différent.
La résolution est comme un 5x5x5
J'aime beaucoup ce twist, bien que le design est un peu différent que celui d'origine mais il est néanmois joli. C'est un puzzle de très bonne qualité
mais reste fragine, il faut le manipuler avec douceur . La version origine de Tony daté en 2004 , le design est légèrement différent.
La résolution est comme un 5x5x5
 Ball-in-cube
Ball-in-cube
 C'est le même style que l'Overlapping, aulieu d 'avoir des pièces carrés au centre le Ball-in-cube (Tony 2008) ont des pièces bombées (rondes) c'est tout. Mais le puzzle est plus fragine que Overlapping
il faut donc le manipuler avec douceur.... Pour bien faire des rotation , il faut bien alligner les centres.
Pour la résolution c'est simplement un 5x5x5 . En resumer c'est un puzzle de très bonne qualité, donc il faut en avoir un dans la collection
C'est le même style que l'Overlapping, aulieu d 'avoir des pièces carrés au centre le Ball-in-cube (Tony 2008) ont des pièces bombées (rondes) c'est tout. Mais le puzzle est plus fragine que Overlapping
il faut donc le manipuler avec douceur.... Pour bien faire des rotation , il faut bien alligner les centres.
Pour la résolution c'est simplement un 5x5x5 . En resumer c'est un puzzle de très bonne qualité, donc il faut en avoir un dans la collection
Ghost Pocket
 Ca fait des années que j'attends la sortie de ce twist, après la sortie du Mirror Block Pocket je me demande qu'est ce qu'on attend pour sortir le
Ghost Pocket ? puis récement FangShi sort ce puzzle en masse , mais la version de FangShi comporte des 'bugs' : Les rotations se bloquent, se coincent... imposible de faire 360° sans se forcer !!, et certaines pièces
ne s'emboîtent pas laissant ainsi des trous !, on voit l'intérieure etc... Bref pas très terrible, de même pour la version de VirustCube. En fait, VirustCube achète les cubes de FangShi et colle son logo dessus c'est tout !!
Ca fait des années que j'attends la sortie de ce twist, après la sortie du Mirror Block Pocket je me demande qu'est ce qu'on attend pour sortir le
Ghost Pocket ? puis récement FangShi sort ce puzzle en masse , mais la version de FangShi comporte des 'bugs' : Les rotations se bloquent, se coincent... imposible de faire 360° sans se forcer !!, et certaines pièces
ne s'emboîtent pas laissant ainsi des trous !, on voit l'intérieure etc... Bref pas très terrible, de même pour la version de VirustCube. En fait, VirustCube achète les cubes de FangShi et colle son logo dessus c'est tout !!
En résumé: le Ghost Pocket n'a pas un core adapté ! il fallait prendre le core 2x2x2 de WitEden ou QiYi.
Ce que je ne comprends pas c'est qu'il y a des cores qui fonctionnent parfaitement bien pour 2x2x2, et FangShi n'a pas utilisé !!!
Ghost Pocket = , production=
, production=
Tangram
 Voici un très joli twist, vraiment joli
Voici un très joli twist, vraiment joli
 Octo Star
Octo Star
 C'est joli ce twist, un design ressemble un peu l'Hexaminx ... vraiment joli, en plus des rotations standards on peut tourner les faces à 45° , ce
qui fait que le cube change de forme, jumbling sommets<->arêtes comme le Mixup ... un twist de très bonne qualité, il faut donc absolument en avoir un.
C'est joli ce twist, un design ressemble un peu l'Hexaminx ... vraiment joli, en plus des rotations standards on peut tourner les faces à 45° , ce
qui fait que le cube change de forme, jumbling sommets<->arêtes comme le Mixup ... un twist de très bonne qualité, il faut donc absolument en avoir un.
Bagua
 Un très joli cube.Tout d'abord si vous voulez ce cube achetez la version à 6 couleurs (sans stickers) en effet avec des petites pièces les stickers se décollent et on les perd facilement ...
Et puis il faut lubrifier un peu et tournez doucement car ça peut popper !! et il n'est pas évident d'assembler le cube vu qu'il y a beaucoup de pièces (140), en un mot soyez prudent.
C'est un twist de type "labyrinthe" (qui bloque les rotations) !!! pour ce genre de twist il n'y a pas d'algorithme de résolution !!! , on voit sur youtubes des tuto pour la résolution de ce twist c'est un peu de la tricherie !! en effet ils s'arrangent pour avoir suffisamment de rotations pour revenir à la forme cubique !! (=faux mélange) .
Mais une fois à la forme cubique , on peut parler de la résolution . La résolution est très longue puisqu'il y a beaucoup de pièces à ranger.
Un très joli cube.Tout d'abord si vous voulez ce cube achetez la version à 6 couleurs (sans stickers) en effet avec des petites pièces les stickers se décollent et on les perd facilement ...
Et puis il faut lubrifier un peu et tournez doucement car ça peut popper !! et il n'est pas évident d'assembler le cube vu qu'il y a beaucoup de pièces (140), en un mot soyez prudent.
C'est un twist de type "labyrinthe" (qui bloque les rotations) !!! pour ce genre de twist il n'y a pas d'algorithme de résolution !!! , on voit sur youtubes des tuto pour la résolution de ce twist c'est un peu de la tricherie !! en effet ils s'arrangent pour avoir suffisamment de rotations pour revenir à la forme cubique !! (=faux mélange) .
Mais une fois à la forme cubique , on peut parler de la résolution . La résolution est très longue puisqu'il y a beaucoup de pièces à ranger.
Ce cube engendre des singularités vu qu'il y a des rotations à 45° on peut donc:
Soit fixer la singularité pendant la résolution, dans ce cas on doit reconnaitre qu'on a une singularité
Soit fixer la singularité après la résolution, dans ce cas la formule de correction est très très longue
Pour résumé : le Bagua est un twist intéresssant mais malheureusement c'est un twist de type labyrinthe, il faut donc imposer, dans le mélange à utilier peu de rotations à 45° ou le mélange doit garder la forme cubique... etc ...
NOTE: Le Bagua, le Curvy Copter III, ... ont le même style que le Square-1, seulement pour le Square-1 quelque soit le mélange on peut toujours passer à la forme cubique.
Sun Cube
 Voici le Sun Cube, qui ressemble beaucoup au OctoStar
Voici le Sun Cube, qui ressemble beaucoup au OctoStar
 Curvy Copter III
Curvy Copter III
 Voici un twist très intéressant, une fois mélangé il est vraiment joli, plein de motifs, et puis comme tous les Copters il a la possibilité de jumbling !
c'est une propriété extêmement noble pour un twist. La résolution comme vous attendez c'est difficile , l'histoire de jumbling rend le twist particulièrement intéressant sur tout quand il produit de patité
et qu'on ne commprend absolument rien d'où ça sort, d'où ça vient et pourquoi ?? ....
Voici un twist très intéressant, une fois mélangé il est vraiment joli, plein de motifs, et puis comme tous les Copters il a la possibilité de jumbling !
c'est une propriété extêmement noble pour un twist. La résolution comme vous attendez c'est difficile , l'histoire de jumbling rend le twist particulièrement intéressant sur tout quand il produit de patité
et qu'on ne commprend absolument rien d'où ça sort, d'où ça vient et pourquoi ?? ....
 Les fruits ...
Les fruits ...
 Fanxin a sorti une serie de 6 fruits (3x3x3) sauf le banane 2x2x3 pour la collections. Ces twists ressemblent beaucoup de vrais fruits !!
On les trouve sur les sites chinois...
Fanxin a sorti une serie de 6 fruits (3x3x3) sauf le banane 2x2x3 pour la collections. Ces twists ressemblent beaucoup de vrais fruits !!
On les trouve sur les sites chinois...

- Pomme
- Poire
- Banane
- Citron
- Orange
- Pêche
 Ce sont de twists de très bonne qualité, très bon plastique, rotations fluides ...
Il faut donc en avoir tous pour la collection.
Ce sont de twists de très bonne qualité, très bon plastique, rotations fluides ...
Il faut donc en avoir tous pour la collection.












