Préliminaire
Principe de relativité :
Ce principe dit que les lois de la nature ont la même forme dans R et dans R',
autrement dit si dans R on a la relation:
x = 2VR'/R cos t' + k ex'
alors dans R' on aura
x' = 2VR/R' cos t + k ex
L'invariant d'intervalle :
On appelle S² = c²t² - x² l'intervalle
donc dans R' on a
S'² = c²t'² - x'²
L'invariant d'intervalle signifie qu'on ait
S² = S'²
démontration :
On cherche une relation entre S² et S'² , on ne va pas casser la tête et compliquer la vie , on cherche la relation du type
S² = kS'²
Si on trouve tant mieux sinon on se débrouillera autrement !!!!
Voyons ce k, normalement il doit être en fonction de O' (x=coordonnée), du t=temps et de la direction de la vitesse VR'/R
* Comme l'espace est homogène , n'importe quel O' convient, donc k ne dépend pas de x=coordonnée
* Comme le temps est homogène , n'importe quel moment t convient, donc k ne dépend pas t
* Comme l'espace est isotope , n'importe quelle direction convient, donc k ne dépend pas la direction de VR'/R
finalement k dépend seulement le module de VR'/R
d'où
S² = k(VR'/R) S'²
Considèrons trois référentiels R, R', R"
S² = k(VR'/R) S'²
S² = k(VR"/R) S"²
S'² = k(VR"/R') S"²
ce qui donne
1 = k(VR'/R) S'² / k(VR"/R) S"²
k(VR"/R) = k(VR'/R) S'² /S"²
k(VR"/R) = k(VR'/R) k(VR"/R')
k(VR"/R) / k(VR'/R) = k(VR"/R')
le membre de droite de cette égalité le k dépand de VR'/R, VR"/R et aussi l'angle θ entre VR'/R et VR"/R
mais le membre de gauche ne dépend pas de θ donc k(VR'/R)=k=constant
finalement
k/k = k
k=1
on a bien
S² = S'²
La transformation de Lorentz
Einstein est l'une des parsonnes qui a osé toucher le fondement de la physique Newtonienne...
L'expérience prouve, ( la réalité, la vérité ) que la vitesse de la lumière est la même dans tout référentiel inertiel (galiléen).
Or la formule des vitesses, change la vitesse de la lumière quand on passe d'un référentiel à un autre, donc la formule est fausse par consequence la TG est fausse aussi puisque la formule des vitesses vient de là. . Il faut donc absolument remplacer TG par une autre transformation qui laisse invariant la vitesse de la lumière.
Voyons ....
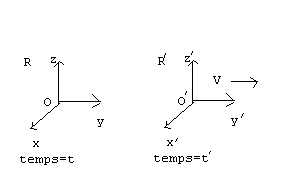
On se donne deux référentiels (galiléens bien sûr) R(x,y,z), t et R'(x',y',z') , t', où le référentiel R' a un mouvement rectiligne uniforme (par rapport à R) c'est à dire son origine O' a un mouvement rectiligne uniforme (par rapport à R). dans le sens Ox de vitesse constante V = VR'/R
On veut trouver une transformation qui fait passer de R à R' en laissant invariant la vitesse de la lumière .
Première méthode (classique)
On va chercher la transformation de la forme
ct' = a (ct) - b x (1)
x' = -b (ct) + a x (2)
puis en utilisant le principe de la relativité pour trouver les paramètres a,b
Allons y....
Un observateur P dans R voit le point O' ainsi:
x = Vt (car O' déplace à la vitesse V par rapport à R)
et x' = 0 car O' est fixe dans R'
(2) donne
0 = -b ct + a Vt (c'est ici l'intérêt d'avoir le signe '-' devant x : -bx)
b = aV/c
En remplaçant la valeur de b dans notre systeme , ça donne
ct' = a (ct) - aVx/c
x' = -aV (ct)/c + a x
puis inversons le systeme
ct' + aVx/c = a (ct)
ct' + V/c.x' + aV² (ct)/c² = a (ct)
ct' + V/c.x' = a (ct) - aV² (ct)/c²
ct' + V/c.x' = a (ct)[1 - V²/c²]
ct = [ct' + Vx'/c]/a[1 - V²/c²]
d'autre part
x' = -aV (ct)/c + a x
x'+ aV (ct)/c = a x
x'+ aV/c . [ct' + Vx'/c]/a[1 - V²/c²] = a x
x'+ [Vct'/c + V²x'/c²]/[1 - V²/c²] = a x
x'+ Vct'/c[1 - V²/c²] + V²x'/c²[1 - V²/c²] = a x
Vct'/c[1 - V²/c²] + x'/[1 - V²/c²] = a x
V/c.ct'/a[1 - V²/c²] + x'/a[1 - V²/c²] = x
x = [Vct'/c + x']/a[1 - V²/c²]
finalement le systeme inverse est
ct = [ct' + Vx'/c]/a[1 - V²/c²]
x = [Vct'/c + x']/a[1 - V²/c²]
or
ct' = a(ct - Vx/c )
x' = a(-Vct/c + x)
le principe de relativité (x'->x, t'->t, V-> -V) donne
ct = a(ct' + Vx'/c )
x = a(Vct'/c + x')
ce qui impose que
a = 1/a[1 - V²/c²]
a² = 1/[1 - V²/c²]
Finalement on trouve
ct' = γ(ct - Vx/c)
x' = γ(-Vct/c + x )
avec
Deuxième méthode (classique)
On va chercher la transformation de la forme
ct' = a(ct) - bx (1)
x' = -b(ct) + ax (2)
puis en utilisant l'invariant de l'intervalle pour trouver les paramètres a,b
Allons y....
Un observateur P dans R voit le point O' ainsi:
x = Vt (car O' déplace à la vitesse V par rapport à R)
et x' = 0 car O' est fixe dans R'
(2) donne
0 = -b ct + a Vt (c'est ici l'intérêt d'avoir le signe '-' devant x : -bx)
b = aV/c
En remplaçant la valeur de b dans notre systeme , ça donne
ct' = a(ct) - aVx/c
x' = -aV(ct)/c + ax
Calculons
c²t'² = a² c²t² - 2a² ctVx/c + a²V²x²/c²
x'² = a²V² c²t²/c² - 2a²Vctx/c + a²x²
c²t'² - x'² = a²c²t²(1 - V²/c²) - a²x² (1 - V²/c²)
c²t'² - x'² = a²(1 - V²/c²) [c²t² - x²]
L'invariant de l'intervalle impose que
a²(1 - V²/c²) = 1
soit
Finalement on trouve
ct' = γ(ct - Vx/c)
x' = γ(-Vct/c + x )
avec
Troisième méthode (moderne)
On ne va pas checher n'importe où notre transformation , mais on va la chercher parmi les transformations de la forme:
ct' = chµ (ct) - shµ x
x' = -shµ (ct) + chµ x
si on trouve, on s'arrête et on est content !! , sinon , bah ... on se débrouillera autrement c'est tout!
On est des physiciens , on fait ce qu'on veut pourvu qu'on arrive !! :-D :-D
Donc notre système est
ct' = chµ (ct) - shµ x (1)
x' = -shµ (ct) + chµ x (2)
Il faut trouver µ ou plus axactemnet chµ et shµ.... Allons y ...
Un observateur P se place dans R, et voit O' ainsi:
xO'=Vt car R' déplace avec une vitesse V par rapport à R,
et un observateur P' dans R', et voit O':
x'O'=0 car O' ne bouge pas dans R'.
donc (2) donne
0 = -shµ (ct) + chµ Vt ; c'est ici l'intérêt d'avoir le signe'-' devant shµ: -shµ
V/c = shµ/chµ
V/c = thµ
or
ch²µ - sh²µ = 1
ch²µ/ch²µ - sh²µ/ch²µ = 1/ch²µ
1 - th²µ = 1/ch²µ
ch²µ = 1/(1-th²µ)
on ne prend pas la valeur négative -√ car chµ ≥ 1 et
remplaçons tout ça dans notre système:
ct' = chµ (ct) - shµ x
x' = -shµ (ct) + chµ x
et voilà notre nouvelle transformation
Posons
et on a
t' = γ(t - Vx/c²)
x' = γ(-Vt + x)
C'est notre nouvelle transformation, la tranformation de Lorentz
Remarque
1. On peut retrouver la transformation de Galilée à partir de la transformation de Lorentz en faisant c=∞ et γ->1 c'est quand même bien ça prouve qu'on est sur la bonne voie, la transformation de Galilée n'est qu'une approximation valable pour des petites vitesses.
2. La transformation inverse est facile à trouver il suffit de remplacer:
prime par non-prime, non-prime par prime et V' = -V
t' = γ(t - Vx/c²)
x' = γ(-Vt + x)
l' inverse
t = γ(t' + Vx'/c²)
x = γ(Vt' + x')
Attention !! ne pas confondre le système inverse avec le système "synonyme" ou "homologue" (principe de relativité)
Le principe de relativité donne le système homologue :
t = γ(t' - Vx'/c²)
x = γ(-Vt' + x')
3. γ nous montre qu'aucun corps peut se déplacer à une vitesse plus grande que la lumière !!
4. La notation x, x'
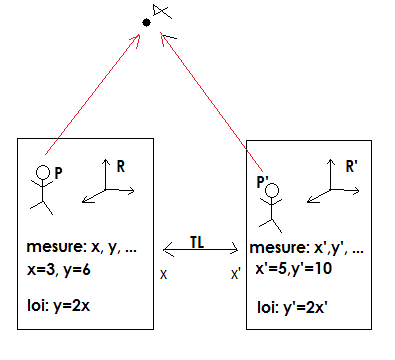
x: Un observateur P dans R mesure α
x': Un observateur P' dans R' mesure α ou c'est pareil: P se place dans R' et mesure α , on dit que P a fait un changement du repère il passe de R à R'.
La transformation de Lorentz permet à P et P' se communiquer. par exp
P telephonne à P' et dit " je parie que vous trouvez x'=5 et y'=10 comme résultat " (grâce à TL, P prédit x',y')
De même P' telephonne à P et dit " je parie que vous trouvez x=3 et y=6 comme résultat " (grâce à TL ou son inverse P' prédit effectivement ce résultat)
Notation matricielle ou tensorielle
La tranformation de Lorentz en notation matricielle ou tensorielle
x0 = ct , x1 = x , x2 = y , x3 = z
x'0 = γx0 - γβx1
x'1 = -γβx0 + γx1
x'2 = x2
x'3 = x3
En notation matricielle
X = (x0, x1, x2, x3)
X' = (x'0, x'1, x'2, x'3)
X' = LX
L désigne la matrice de Lorentz , i=ligne, j=colonne
En notation tensorielle