PHYSOTOP

L' espace de Riemann

Considèrons une surface V paramétrée par un système de coordonnées curvilignes xⁱ , on plonge cette surface dans l' espace euclidien Rⁿ⁺¹. Si on désigne u^k les coordonnées cartésiennes usuelles d'un point M(u⁰,u¹, ...,uⁿ) de Rⁿ⁺¹, le plongement implique qu'on aie les relations suivantes:

u^k = u^k (x⁰,x¹, ...,xⁿ)

les coordonnées cartésiennes sont en fonctions des coordonnées curvilignes, et le point M(u⁰,u¹, ...,uⁿ) devient M(x⁰,x¹, ...,xⁿ)
La donnée d'une surface V c'est la donnée de son paramétrage xⁱ, cad la donnée de n fonctions f^k(x⁰,x¹, ...,xⁿ) de variables xⁱ telles que

u^k = f^k (x⁰,x¹, ...,xⁿ) mais par abuse de langage on écrit

u^k = u^k (x⁰,x¹, ...,xⁿ) pour dire que les u^k sont en fonction des xⁱ
u^k = u^k (xⁱ)

nous allons maintenant voir quelle est la forme de la métrique ds² de V.

on a:
du^k = ∂_α(u^k) dx^α

ds² = (du⁰)² + (du¹)² + ...+(duⁿ)² ; on est dans l'environnement de V qui est Rⁿ⁺¹
en développant ça donne
ds² = g_{α β} dx^αdx^β
où g_{α β}(x⁰,x¹, ...,xⁿ) sont des fonctions de xⁱ le paramétrage de V, grâce au plongement on a pu définir le ds² de V.

on a
dM = ∂M/∂x^α dx^α
si on pose

e_i = ∂M/∂xⁱ = ∂_iM le répère (M, e_i) s'appelle repère locale (ou naturel) de V en M , e_i s'appelle base covariante en M. Les vecteurs e_i engendrent un esv T_M nommé l'espace tangente de V en M, et on voit que

g_{i j} = e_i . e_j produit scalaire
et
dxⁱ = coordonnées de dM dans la base e_i

en effet
dM = dxⁱ e_i
dM.dM = dM² = dxⁱ e_i dx^j e_j
or

dM² = ds² donc g_{i j} = e_i . e_j

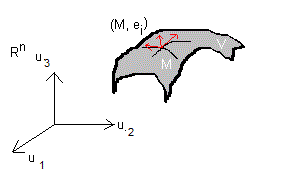
Le couple (V,ds²) avec
ds² = g_{α β} dx^αdx^β
où g_{α β}(x⁰,x¹, ...,xⁿ) sont des fonctions de xⁱ le paramétrage de V
constitue un exemple d'un espace de Riemann

Note
On démontre que le ds² ne dépend pas du paramétrage xⁱ de V , il est propre, intrinsèque à V.

Composantes contravariantes et covariantes

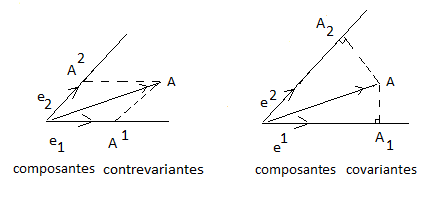
Pour un vecteur A de T_M on peut le répèrer par (A⁰,A¹, ...,Aⁿ) mais aussi par A = (A₀,A₁, ...,Aⁿ) on a donc:

A = A^α e_α et A = A_α e^α
et
A_i = A.e_i (par définition de A_i)
d'où

A_i =A^α e_α .e_i

donc
A_i = g_iαA^α
ou encore
Aⁱ = g^iαA_α
g^ij est la matrice inverse de g_ij :

de même
A = Aⁱ e_i = g^iαA_α e_i
d'où
e^α = g^iαe_i
à chaque base covariante e_i on associe une base contravariante eⁱ de façon suivante:
eⁱ = g^iαe_α
et
A = A_α e^α
Les composantes Aⁱ se nomment contravariant et A_i covariant du vecteur A.

Au lieu de prendre une surface on prend une variété (plusieurs morceaux de surfaces collées , chaque morceau est gèré par un système de coordonnées curvilignes) donc pour un morceau de la variété on tombe sur le cas précédant càd un morceau de surface paramétrée par un système de coordonnées curvilignes xⁱ reliant aux coordonnées cartésiennes u^k.
u^k = u^k (x⁰,x¹, ...,xⁿ)
à partir de là on trouve la métrique ds² de V et les g_ij .
On a plongé V dans l' esv euclidien Rⁿ , la métrique de Rⁿ , δ_ij (ds² = δ_{α β} du^αdu^β) et la métrique de V , g_ij sont reliées par:

g_ij = δ_αβ ∂_iu^α ∂_ju^β
(*)

En fait, on peut définir un espace de Riemann, sans passer par le plongement, on se donne simplement une variété V et sa métrique g_ij sans l'obligation de férifier (*) mais doit vérifier quand même un certain nombre de conditions du genres:
1. Symétrique: g_ij = g_ji.
2. g_ij de classe ≥ C²
3. dét(g_ij) ≠ 0 etc ... en fait on impose à g_ij tout ce qu'il faut pour ne pas avoir des problèmes !!!

Exemples de l'espace Riemannien

l'espace de Minkowski (V,ds²) où
ds² = (dx⁰)² - (dx¹)² -(dx²)² -(dx³)²
x⁰ = ct , x¹ = x , x² = y , x³ = z

La tranformation de Lorentz
x' ⁰ = γx⁰ - γβx¹
x' ¹ = -γβx⁰ + γx¹
x' ² = x²
x' ³ = x³





En notation tensorielle


Où L est la matirce de Lorentz


l'espace de Schwarzschild (V,ds²) où
ds² = e^a(dx⁰)² - e^b(dx¹)² -r²(dx²)² -r²sin(θ)²(dx³)²
x⁰ = ct , x¹ = r , x² = θ , x³ = φ

Commentaire

Une variété V est en fait un ensemble de morceaux de Rⁿ collés entre eux, et chaque morceau gèré (paramétré) par un système de coordonnées curviligne xⁱ .
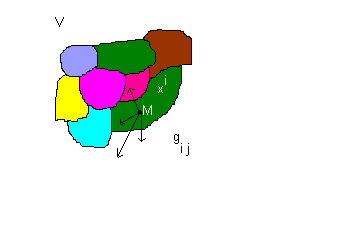
en chaque point attachés plein de vecteurs, tenseurs .... et on veut faire des calculs sur ces objets. Pour faire des calculs le plus simple c'est d'attacher en chaque point de V un esv euclidien noté T_M et les calculs se font dans cet esv. dim T_M = dim V

dim V=1
dim V=2
dim V=3
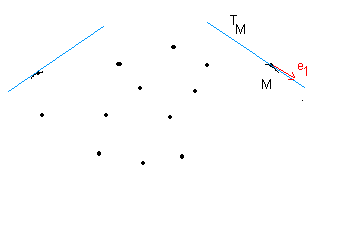
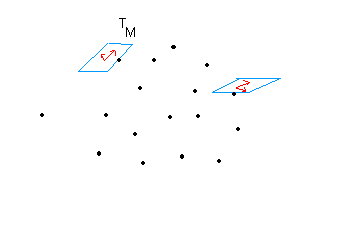
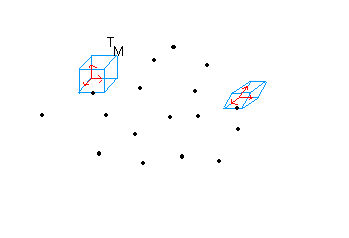
Pour comprendre, imaginez votre maison composée de plusieurs pièces: la cusine, le salon, la salle de bain, les chambres .... dans chaque pièces disposée une calculatrice. Quand vous êtes dans la salle de bain pour calculer vous prenez la calculatrice sur place et faites des calculs, puis quand vous êtes au salon, pareil pour caculer vous prenez la calculatrice du salon et faites des calculs .... Bien que les calculatrices sont toutes différentes mais peu importe l'essentiel c'est que vous arrivez à calculer !!! Tel est l'espace de Riemann
maison = Variété
pièce = morceau de Rⁿ
calculatrice = métrique g_{i j}
Dans un esv euclidien: votre maison a une seule pièce ! une seule calculatrice !! maison = esv
calculatrice = δ_{i j}

---

[1]

Accueil

DMJ: 19/07/2018