Un référentiel
vitesse, trajectoire ...
Avant tout, il faut se donner un " cadre " pour travailler, c'est par rapport à ce cadre qu' on fait des mesures, des observations ... c'est ce qu'on appelle (ce cardre) un référentiel . Par exemple , si par rapport à la Gare qu'on mesure la vitesse du train, alors la Gare est un référentiel dans lequel on étudie le train. Une personne qui marche dans le train, on peut étudier (le mouvement par exp) cette personne par rapport au train ou par rapport à la Gare. .... En tout cas il faut préciser par rapport à quoi avant d' engarer la discution!!
Un référentiel est en fait une sort de repère R(x,y,z) muni un temps t . Le repère R(x,y,z) est "collé" dans le référentiel qui peut être la Gare, une maison, la Tour Eiffel ... ou n'importe quoi qui soit fixe sur la terre. Un référentiel est donc un couple (R,t) où R=un repère et t= le temps.
Le mouvement
La notion de mouvement est relative, on bouge par rapport à quelque chose. Une voiture roule, le conducteur bouge par rapport à la gare, à la Tour Eiffel , à votre maison .... mais fixe par rapport au volant !!!
Donc parlez de mouvement il faut préciser par rapport à quoi, sinon ça veut rien dire !!
Mais alors la phase : " La voiture roule à 100km/h " tout le monde comprend, mais par raport à quoi on a 100km/h ???? Eh bien , C'est par raport à la Tour Eiffel !! ou encore c'est par rapport à la gare, à votre maison ... la voiture s'éloigne de plus en plus de votre maison ... En fait c'est par rapport à n'importe quoi, qui soit fixe sur le sol (sur la terre) !!!
Donc " La voiture roule à 100km/h " c'est par rapport à votre maison sous entendu.
L'Equation de mouvement
Vous savez maintenant pour parler du mouvement il faut préciser par rapport à quoi, il faut donc donner un repère, un référentiel c'est par rapport à ce repère, ce référentiel qu'on travaille, qu'on étudie .....
On se donne donc un repère R(x,y,z) mais ce repère doit être figé sur la terre, collé sur une maison ... , l'objet m est répèré par ses coordonnés x,y,z.
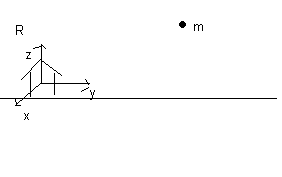
Les x,y,z sont en fonction du temps t puisque m bouge !!! donc
x= x(t), y=y(t) et z=z(t)
Les x(t), y=y(t) et z=z(t) nommée les équations du mouvement, c'est donc une relation entre les coordonnées x,y,z et le temps t
par exemple
x = gt²/2
ou encore
x = 100t
La vitesse
La vitesse est aussi une notion relative !!. Un train T va à 100km/h , une parsonne A marche dans le train à 5km/h . On comprend bien que ca signifie:
VT/G = 100km/h la vitesse du train T par rapport à la gare G
VA/T = 5km/h la vitesse de A par rapport au train T
Mais comment trouve -t-on la vitesse ? c'est très simple. R est donné , m est donné (donc les x(t) ,y(t), et z(t) sont donnés ), la vitesse de m par rapport à R est par défition:
VT/R = (dx/dt, dy/dt, dz/dt) !!!
donc il faut trouver les coordonnées de m dans R puis les dérive .
exemple
on a
x = 100t (R = collé à la Tour Eiffel et l'axe x dans le sens de mouvement)
v = 100 (Vm/R avec unité=m/s bien sur)
x = gt²/2 (R = collé à la Tour Eiffel et l'axe x dans le sens vertical-bas)
v = gt (Vm/R)
L' accélération
C'est simplement la dérivé de la vitesse !!
l'accélération de m par rapport à R est par défition:
γ m/R = (dx²/dt², dy²/dt², dz²/dt²)
simplifion l'écriture
γ = dv/dt
Relation fondamentale
Un mouvement est donc repésenté par x(t) , y(t) , z(t) on sait que la cause du mouvement est la force. La question naturelle est la suivante: " quelle est la relation entre le mouvement et la force ? " cad quelle est la relation entre (x,y,z) et f ?
Eh bien c'est
f = m γ (Newton)
Autrement dit si on donne f on connaîtra γ donc les x,y,z cad les équations du mouvement
Si on donne γ cad les équations du mouvement on peut alors caculer f
La trajectoire
La trajectoire est le chemin que m a empreinté pour aller de A à B. C'est donc une relation entre les coordonnées.
f(x,y,z) = 0
Elle peut etre : une droite, un segment de droite, un cercle, une ellipse, un parabole ....
exp:
x² + y² = R² (la trajectoire est un cercle de centre O et de rayon R)
x = 3z² (la trajectoire est un parabole dans le plan (x,z) )
ne confendez pas la trajectoire et le mouvement, la trajectoire c'est f(x,y) = 0 , le mouvement c' est x = f(t) , y = g(t)
trajectoire: x² + y² = R²
mouvement:
x = gt²/2
y=100t
Type de mouvement
x = vt mouvement rectiligne uniforme, vitesse v= constante
x = gt²/2 mouvement rectiligne varié, accélération γ = constante
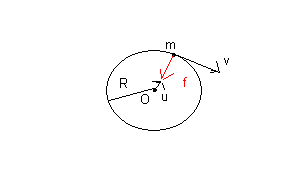
mouvement circulaire uniforme de vitesse v
x = R cos(vt/R)
y = R sin(vt/R)
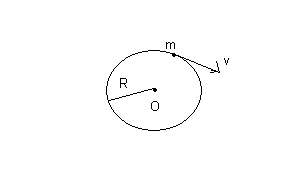
On sait que ce type de mouvement est causé par la seule force:
f = - m v²/R u
Référentiel d'inertie
On ne va pas prendre R quelconque, mais un référentiel tel que les lois de la physique soient le plus simple possible. Autrement dit s'il n'y a pas de force (extérieur) qui exerce sur M alors, soit M est immobile (v=0) soit il prend un mouvement rectiligne uniforme (v=constante non nul). ces référentiels s'appllent référentiel d'inertie. On admet qu'il en existe dans la nature. Et heureusement (on a de la chance!) la terre est (pratiquement) un référentiel d'inertie !!
Remarque: il est possible que M soit en mouvement, alors qu'il n'y aucune force (cas v=constante ≠ 0)
[1]
Accueil
DMJ: 23/06/2015