Exo fondamentaux
Chute libre
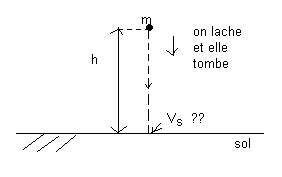
On lache une pierre de masse m d'une hauteur de h , quelle est sa vitesse Vs lorsqu'elle touche le sol ??
Solution
Analyser le problème
La première chose à faire, c'est de comprendre ce qui passe, comprendre l'expérience, compredre le phénomène .... dans notre exercice c'est très simple à comprendre rien à dire.
La deuxième chose à faire , c'est qu' il faut savoir ce qu'on a, (les donnés du problème) et ce qu'on cherche . Pour nous les données sont: m la masse de la pierre, h la hauteur du chute et c'est tout !! Et ce qu'on cherche c'est la vitesse Vs lorsque la pierre touche le sol.
Comment s'en sortir ?? si vous avez lu les autres chapitres, vous pouvez vous en sortir !!!
Il y a 3 façons de s'en sortir !!!
Méthode 1 (énergie potentielle)
Préparation: Avant de faire des calculs , il faut bien préciser le repère R !! c'est le repère dans lequel on travaille , car les équations, les vitesses , les énergies .... sont tous écrits dans un repère !!! on prends donc un repère "collé" à votre maison, adaptable, orienté de tel sort que les équations soient le plus simple possible.
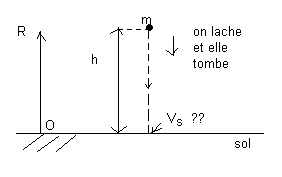
Pour nous on va prendre le repère R comme indique la fig "meca12" , c'est le plus naturel et le plus adapté pour notre problème.
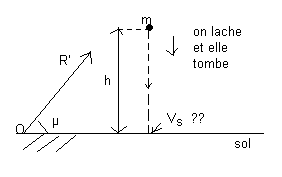
On ne va pas quand même choisir le repère R' , l'écriture dans ce repère est trops compliqué Vs/R' = - Vs/Rsin(µ) , ne compliquons donc pas la vie pour rien !!
Analysons la chose: La pièrre se trouve à une altitude h, la Terre lui attribue une énergie potentielle pesenteur Ep
Ep = mgh
et la pierre tombe (elle bouge) donc elle acquiert une énergie cinétique Ec
Ec = mv²/2
le théorème 1 nous dit : Ec + Ep = Const
autrement dit:
Ec,i + Ep,i = Ec,f + Ep,f
et voila nous avons prèsque fini , en effect il suffit de calculer ces énergies
Ec,i = 0 car on lache la pierre pas de vitesse initiale v=0.
Ep,i = mgh
Ec,f = m V²s/2
Ep,f = 0 car h=0
d'ou
0 + mgh = m V²s/2
2gh = V²s
Remarque important: on voit que la vitesse arrivant au sol Vs ne dépend pas de la masse m de l'objet !! c'est bizarre hein ? car on voit bien qu'une bille tombe plus vite qu'une feuille !!! mais l'explication de ce phénomène c'est une autre histoire .
----
Méthode 2
On va utiliser le théorème de l'énergie cinétique.
Analyser des forces
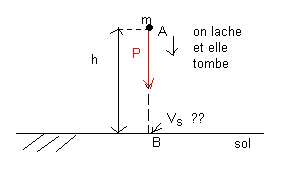
La première chose à faire, c'est d'analyser des forces qui appliquent sur m , dans notre cas il y a une seule force P (son poids) qui applique sur m. Et la pierre déplace d'une distance h , le tavail de P est donc
W = P.AB = P.h cos(P,AB) = mg.h car angle(P,AB)=0
Ec,f = m V²s/2
Ec,i = 0 pas de vitesse initiale
théorème de l'énergie cinétique dit:
Ec,f - Ec,i = W
m V²s/2 = mg.h
V²s = 2g.h
----
Méthode 3
On va utiliser la relation fondamentale.
Analyser des forces
Analysons des forces qui appliquent sur m , dans notre cas il y a une seule force P=mg (son poids) qui applique sur m.
La relation fondamentale nous dit:
f= m γ
donc
P = m γ
mg = m γ
g = γ
g = γ
d'où
γ = dv/dt = g ===> v = gt + V0
or pour t=0, v(0) = 0 pas de vitesse initiale
v(0) = V0
0 = V0
v = gt
v = dx/dt = gt ===> x = gt²/2 + x0
or pour t=0, x(0) = h ; on est en altitude h
x(0) = x0
h = x0
x = gt²/2 + h
On a:
v = gt
x = gt²/2 + h
Bricolons
v²=g²t²
2g(x-h)=g²t²
2g(x-h)=v² : cette relation est valable pour n'importe quel x il suffit de prendre x-h=h on a:
v² = 2gh
[1]
Accueil
DMJ: 19/07/2018