Le lagrangien
Résumé: axiomes
1) Référentiel galiléen: R(x,y,z),t
2) Transformation Galilée: R(x,y,z),t ==> R'(x',y',z'),t'
3) Le principe relativité galilée: Une loi de la physique a la même forme dans tous les référentiels galiléens R
Caractéristiques d'une particule M:
4) Impulsion: p=mv
5) Energie:
6) Loi fondamentale (Newton) : f = mγ
7) Travail
8) La Gravitation (Newton):
Le lagrangien
Les physiciens aiment bien unifier les choses. On aimerait bien unifier 4) et 5) et remplacer l'équation 6) par une autre, plus jolie, plus élégants, plus universel...
Pour cela on stipule qu'une particule est caraterisée par une fonction L(x,v) (au lieu de E et p) nommée le lagrangien de M .
Par définition l'impulsion de M est:
p = ∂vL (Notation: ∂v = ∂/∂v)
et son énergie:
E=v.p-L
on a donc unifié p, E en une seule grandeur L.
L'équation 6) s'appelle l'équation du mouvement, pour la remplacer on utilise le principe "le moindre action" :
A chaque particule M on associe une action S définie par:
S = ∫ L(x,v) dt
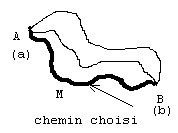
Parmi les trajectoires possibles faisant passer de A à B la particule choisit celui qui a le moindre action cad δS = 0.
A partir du principe le moindre action, nous allons déduire les équations de Lagrange.
S = ∫ab L(x,v) dt
δS = ∫ab (∂L/∂x δx + ∂L/∂v δv) dt
c'est δx qu'on va faire varier pour trouver l'équation du mouvement (c'est logique puisque M bouge donc δx varie de plus on impose aux bordes a,b δx(a)=δx(b)=0). Vu l'intégral ça suggère une intégration par partie de ∂L/∂v δv
∂L/∂v ====> d(∂L/∂v )/dt
δv ===> δx
d'où
∫∂L/∂v δv = [∂L/∂v δx] - ∫d(∂L/∂v )/dt δx
δS = [∂L/∂v δx]- ∫[∂L/∂x - d(∂L/∂v)/dt ]δx dt
Le 1er terme du 2e membre est nul car δx(a)=δx(b)= 0 d'autre part l'égalité est vraie pour tous les chemins cad vraie pour quelque soit δx
donc
∂L/∂x - d(∂L/∂v)/dt = 0
ou encore
d(∂L/∂v)/dt = ∂L/∂x c'est l'équation de Lagrange.
Finalement une particule M ayant un lagrangien L son équation de mouvemnt est:
L'intêret dans cette formulation, c'est qu'on voit, dans l'équation du mouvement, L le caractéristique de M, alors que dans 4)5)6) non
REMARQUE: la version vectorielle de dt(∂vL) = ∂xL est
∂v = (∂a,∂b,∂c)
Il faut maintenant retrouver 4)5)6). Voyons, l'expérience montre que, pour une particule libre (ne subie aucune force) le lagrangien vaut:
L=mv²/2
d'ou
p = ∂vL = ∂v(mv²/2) = mv
et
E=v.p-L = mv.v - mv²/2 = mv² - mv²/2 = mv²/2
Pour 6) on pourrait raisonner ainsi:
Une force f est caractérisée par un potentiel U(x,y,z,t) avec f=-gradU. Alors une particule M plongée dans un champs de potentiel U(x,y,z,t) son lagangien dans ce cas vaut:
L=mv²/2 - U(x,y,z,t) et l'équation de mouvement donne
dt(∂vL) = ∂xL
dtp = ∂x(mv²/2 - U) = -∂xU
dtp = -gradU
mdtv = f
mγ=f
Quelques commentaires:
1. Pour retouver l'équation de Newton, on a supposé que la force f dérive d'un potentiel U. Prèsque que toutes les forces de la nature dérive d'un potentiel
il existe rarement des forces qui ne proviennent pas d'un potentiel, et ça ne nous intéresse pas ces forces c'est tout !!
2. La question se pose toute de suite est: comment trouve t-on le lagrangien d'un système ? eh bien, par expérience, par tatonement.
Principe: On met ce qui faut pour avoir ce qu'on veut !!!