Notion de limite
Si on répéte indéfiniment l'opération ...√√√4 on tombe sur 1, en effet
il y a n racine √ , comme
On a donc
On pose: ...√√√4 = 40 , donc 40 est une sorte de limite , une suite infinie d'opération √
Les quatrix
Un quatrix est un nombre qui s'écrit avec quatre chiffres '4' et les 8 opérations suivantes E = { +, -, x, /, √, ab, !, 40 }
Rappel
√4 = 2
23 = 2x2x2 = 8
5! = 5x4x3x2x1 = 120
40 = 1
NOTE:
-Les parenthèses '(', ')' sont autorisées , c'est juste pour la visibilité des lectures.
-Les écritures 44, 444, 4444, ... ne sont pas autorisées
On évite d'utiliser la 8ème opération 40 tant qu'on peut puisque c'est une limite, une suite infinie d'opérations √ .
Donc quand on a une expression sans 40 on la garde plutôt d'utiliser l'expression avec 40, les quatrix qui s'écrivent avec 40 se nomment quatrix pur
Problème : Quels sont les quatrix, qu'on peut atteindre ??
Voici ma liste des quatrix de 0 à 100
0 = 4 - 4 + 4 - 4
1 = 4/4 + 4 - 4
2 = 4/4 + 4/4
3 = √4 + √4 - 4/4
4 = √4 + √4 + 4 - 4
5 = √4 + √4 + 4/4
6 = 4 + √4 + 4 - 4
7 = 4 + √4 + 4/4
8 = 4 + 4 + 4 - 4
9 = 4 + 4 + 4/4
10 = 4 + 4 + 4/√4
11 = 4!/√4 - 4/4
12 = 4(4 - 4/4)
13 = (4! + 4! + 4)/4
14 = 4 x 4 - 4/√4
15 = 4 x 4 - 4/4
16 = 4 x 4 + 4 - 4
17 = 4 x 4 + 4/4
18 = 4 x 4 + 4/√4
19 = 4! - (4 + 4/4)
20 = 4(4 + 4/4)
21 = 4! - (4 - 4/4)
22 = 4! - (4 + 4)/4
23 = 4! - (√4 + √4)/4
24 = 4! - (√4 + √4 - 4)
25 = 4! + (√4 + √4)/4
26 = 4! + (4 + 4)/4
27 = 4! + (4 - 4/4)
28 = 4! + 4 + 4 - 4
29 = 4! + 4 + 4/4
30 = 4! + 4 + 4/√4
31 = 4! + (4! + 4)/4
32 = 4! + 4 + √4 + √4
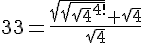
34 = 4! + 4 + 4 + √4
35 = (4!-√4)/√4 + 4!
36 = (4! + 4! + 4!)/√4
37 = 4! + (4! + √4)/√4
38 = 4! + (4! + 4)/√4
39 = √4(4! - 4) - 40
40 = (4+4+√4)4
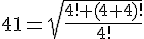
42 = 4! + 4! - (4 + √4)
43 = 4! + 4! - 4 - 40
44 = 4! + 4! - (√4 + √4)
46 = 4! + 4! - (4/√4)
47 = 4! + 4! - 4/4
48 = 4! + 4! + 4 - 4
49 = 4! + 4! + 4/4
50 = 4! + 4! + 4/√4
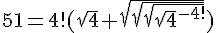
52 = 4! + 4! + √4 + √4
53 = 4! + 4! + 4 + 40
54 = 4! + 4! + 4 + √4
55 = √4(4! + 4) - 40
56 = 4! + 4! + 4 + 4
57 = √4(4! + 4) + 40
60 = 4x4x4 - 4
68 = 44/4 + 4
70 = 4! + 4! + 4! - √4
71 = 4! + 4! + 4! - 40
73 = 4! + 4! + 4! + 40
74 = 4! + 4! + 4! + √4
75 = (40 + 4!) (40 + √4)
76 = 4! + 4! + 4! + 4
77 = (4 - 40)4 - 4
78 = 4(4! - 4) - √4
79 = 4(4! - 4) - 40
80 = √4√4(4! - 4)
81 = (4 - 4/4)4
82 = 4(4! - 4) + √4
83 = (4 - 40)4 + √4
84 = 4(4! - 4) + 4
85 = (4 - 40)4 + 4
86 = 4(4! - √4) - √4
87 = 4(4! - √4) - 40
88 = 4x4! - 4 - 4
89 = 4(4! - √4) + 40
90 = 4! x 4 - 4 - √4
91 = (4 x 4!) - 4 - 40
92 = 4! x 4 - √4 - √4
94 = 4! x 4 - 4/√4
95 = 4! x 4 - 4/4
96 = 4! x 4 - 4 + 4
97 = 4! x 4 + 4/4
98 = 4! x 4 + 4/√4
100 = 4! x 4 + √4 + √4
Les quatrix
I. Initialement on a le chiffre '4' et les 7 opérations { +, -, x, /, √, ab, ! } , la fabrication des quatrix (sans 40) ressemble beaucoups à la construction des nombres constructibles, des radicaux, des propositions (en logique) ...
En effet au départ on a un petit ensemble A, et les opérations E, puis on construit des ensembles de plus en plus grands à partir de ces opérations avec des nombres déjà construits Par exemple pour les nombres constructibles on a:
A = {0,1} ensemble de départ
E = { +, -, x, /, √ } opérations
Et l'ensemble qu'on atteint c'est les nombres obtenus par la règle et au compas !!!
Pour les radicaux on a:
A = {0,1} ensemble de départ
E = { +, -, x, /, n√=racine n-ièm } opérations
Et l'ensemble qu'on atteint c'est les solutions des équations résolubles !!!
Pour les propositions on a:
A = {p,q,r,...} ensemble de départ (infini)
E = {∧ , ∨, ⌉ , → , ↔ } opérations
Et l'ensemble qu'on atteint c'est les propositions en logique.
Un quatrix , c'est:
A = {4} ensemble de départ
E = { +, -, x, /, √, ab, ! } opérations
Et on limite le nombre à longeur 4 (quatre chiffres '4') mais c'est arbitraire on pourrait ne pas limiter sur la longeur (comme les propositions, les nombres constructibles,...) par ex:
Il est donc intéressant de savoir quels sonts les quatrix qu'on peut atteindre ? plus précisement les quatrix de longeur 4 ???
En fabriquant des quatrix , j'ai remarqué qu'il est difficile de former des nombres impairs et certains nombres comme 39, 43, ... semblent impossible d'exprimer en quatre '4' !! (avec ces 7 opérations) Pourquoi ??
J'ai donc émis la conjecture suivante: les nombres
39, 43, 53, 55, 57, 59, 61, 67, 69, 71, 73, 75, 77, 79, 83, 85, 87, 89, 91
sont des quatrix pur (avec 40)
J'ai cherché la réponse pendant longtemps, et posté cette question dans plusieurs forums mathématiques ... mais aucune réponse !!! hummm ....
Il faut croire que la question n'est pas intéressante !!
Puis dernièrement je reprends la question:
1- Pourquoi il est difficile de fabriquer des nombres impairs ?
2- Sur les sites les nombres commes 39,43,... utilisent toujours une 8ème opération ?? il semble que ces nombres sont des quatrix pur
Et je n'ai aucune idée de la façon de démontrer que 39, 43, ... sont des quatrix pur .
Puis d'un seul coup j'ai trouvé la réponse de la question (1), elle est si simple !!!
En effet on part d'un nombre pair 4 et les opérations ne produit que des nombres pairs !!! sauf la division '/' où on peut espèrer avoir un nombre impair comme par ex 10/2 = 5, 22/2 = 11.
On a donc une chance sur 7 , 1/7 de tomber sur '/' et pour '/' on a une chance sur 2, 1/2 d'avoir un nombre impair donc finalement on a 1/7 x 1/2 = 1/14 une chance sur 14 pour fabrique un nombre impair !! c'est pourquoi il est difficile de fabriquer des nombres impairs.
Pour la question (2) , j'écris un script informatique (javascript) qui permet de produire un certain nombres quatrix entre 1 et 100, et le programme ne trouve pas l'expression pour 39, 43, .... ça ne prouve pas l'impossibilité pour ça il faut être sûr que le script donne tous les quatrix entre 1 et 100, mais ça confirme quand même l'idée que pour 39, 43,... c'est impossible, ils sont des quatrix pur .
Le script est ici:
quatrix.js
quatrix.html
Voir la dificulté de produire des nombres impairs, on ajoute une 8ème opération dont le but est de rendre équitable la production des nombres pairs et impairs. la façon la plus simple c'est d'obtenir '1' avec un seul '4'
Il y a plusieurs candidats par exemple
Γ(n)=(n-1)! ==> Γ(√4)=1
[n]=partie entière de n ==> [√√4]=1
etc ...
pour nous ça serait 40 = 1 (pour la raison ...√√√4 = 1)
J'ai du mal à trouver nombre 75 manuellement ... alors j'ai fait un programme
qui exploire certaine possibilité et finalement j'ai trouvé: 75 = (40 + 4!) (40 + √4) Youpi !! Vive l'informatique !!!
Les autres quatrix
Il est remarquable que i et π sont des quatrix !! en effet
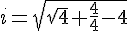
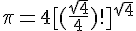
et aussi ...
1260 = [(4!+4)/4]! /4 il suffit de remarquer 7! /4 = 1260
2592 = (4!/4)4. √4
768 = 4 x 4 x 4! √4