Définition de la continuité
Les fonctions continues sont très importantes car elles possèdent beaucoup de propriétés, et puis pratiquement on ne travaille que sur les fonctions continues.
On dit que la fonction f(x) est continue en x0 si
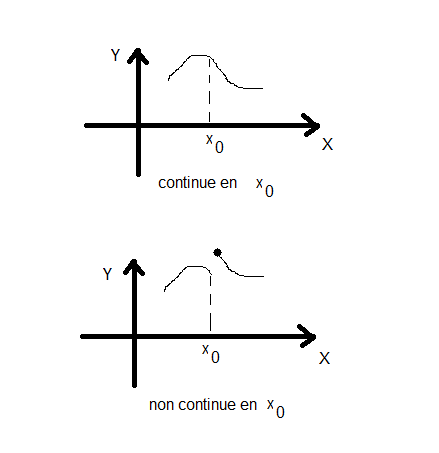
REMARQUE
1. Dire que f(x) est continue en x0 revient à dire que lim f(x) = f(x0) quand x->x0
2. f(x0) doit être défini (existe)
Lorsque f(x) est continue en tout point x0 de l'interval [a,b] on dit que f(x) est continue sur [a,b]
Exemple: f(x) = 2x+5, et f(2)=9 on a
On va montrer cela à partir de la définition, la statégie c'est qu'on va raisonner à l'envers !!
|f(x)-9|<ε
|2x+5-9|<ε
|2x-4|<ε
2|x-2|<ε
|x-2|<ε/2
On voit que notre µ vaut ε/2 donc il suffit de prendre µ=ε/2 (ε est donné) et imposer
|x-2|<µ puis remonte les calculs et on trouve |f(x)-f(2)|<ε
Donc dèsque x est proche de 2, on a f(x) est proche de f(2), c'est bien la définition de la continuité en x0=2
On peut définir la continuité à droite (x->x0+)
et aussi à gauche (x->x0-)
Si k=l on dit simplement que f(x) est continue x0