Les ensembles
E = { x, a, b, y, ....} , E est un ensemble et les x, a, b, y, ... sont des éléments de E
x∈E , x appartient à E
∅ = ensemble vide
P(E) = ensemble des parties de E
|E| = le cardinal de E, le nombre d'éléments de E
Soient E et F deux ensembles
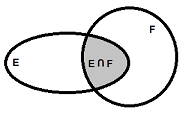
E ∩ F , intersection, E inter F . Si E ∩ F = ∅ on dit que E et F sont disjoints
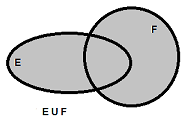
E ∪ F , réunion , E union F
Si A est une partie de E , A ⊂ E, A inclus dans E
l'ensemble des couples (a,b) avec a∈E et b∈F sera noté E x F
 |
 |
| E ∩ F |
E ∪ F |
Relation
Soit E un ensemble, si les éléments de E sont en relation on note xRy , x en reletion avec y
- xRx , réflexive
- xRy ⇒ yRx , symétrie
- xRy et yRz ⇒ xRz transitive
- xRy et yRx ⇒ x=y , anti-symétrie
Relation d'équivalance : réflexive, symétrie, transitive
Relation d'orde : réflexive, anti-symétrie, transitive
Lordre total si on a: xRy ou yRx
Lordre partiel si on trouve au moins un coupe (x,y) qui n'est pas en relation
Les classes d'équivalance
Soient E un ensemble et R une relation d'équivalance
et soit a un élément donné, les éléments x qui sont en relation avec a, xRa forme un ensemble qu'on appelle la classe de a, on note a* (par exp)
a* = { x∈E, xRa }
l'ensemble des classes a*, b* , .... sera noté E/R = {a*, b*, ...}
Les classes possède 2 propriétés
a* ∩ b* = ∅ ils sont disjoints 2à2
a* ∪ b* ∪ ... = E , union des classes donne E
Ainsi les classes forme une partion de E
Un exp d'une relation équivalance
E = Z et
xRy: x-y = 3k , un multiple de 3
Vérifions si c'est une relation d'équivalance
x-x=0 , 0 est un multiple de 3 donc la relation est réflexive
x-y = 3k ⇒ y-x = 3(-k) , donc symétrique
x-y=3k et y-z=3k' ⇒ x-z=3(k+k') , transitive
Ce qui prouve c'est une relation d'équivalance.
la classe de 2 est 2* = { x-2 = 3k} = { ...,2, 5, 8, 11, ...}
il n'y a que trois classes : 0*, 1*, 2*
0* = {x = 3k } = { ..., -3, 0, 3, 6, 9, ...}
1* = {x = 3k + 1} = { ..., -2, 1, 4, 7, 10, ...}
2* = {x = 3k + 2} = { ..., -1, 2, 5, 8, 11, ...}
et on a bien, les classes sont disjointes et la réunion des classes ça donne Z
L'ensemble des classes Z/R = {0*, 1*, 2*} est noté habituellement Z3
[1]
Accueil
DMJ: 19/12/2020

