Les graphes
Graphes eulériens
Une chaîne eulérienne est une chaîne qui passe par toutes les arêtes du graphe, et pour chaque arête elle passe une et une seule fois.
Un cycle eulérien est une chaîne eulérienne avec sommet départ = sommet arrivé (une boucle)
Un graphe G=(V,E) est eulérien s'il existe une chaîne eulérienne ou un cycle eulérien.
Théorème d'Euler
Un graphe connexe est eulérien s' il possède 0, ou 2 sommets de degré impair.Démontration:
Cas 1 :
* Eulérien ⇒ 0 sommet impair: Soit G un graphe eulérien, il existe donc un cycle eulérien µ qui parcourt tout le graphe c'est-à-dire tous les sommets. En démarrant µ en A on revient donc un A en parcourant tous les sommets, cela signifie donc les sommets ont un degré pair puisqu'on arrive puis on repart.* Eulérien ⇐ 0 sommet impair: Soit G un graphe connexe, dont tous les sommets ont un degré pair.
Soient A,T deux points du graphe, puisque G est connexe, il y a une chaîne c entre A et T, on va marquer les arêtes de c comme "utilisé" (fig1), à partir de T on peut toujours continuer (avancer) puisque d°(T) = pair

- à chaque fois on avance, on marque "utilisé" l'arête traversée. (fig2)
on ne peut pas avancer indéfiniment car le graphe est fini (le nombre de sommets est fini), donc on revient forcement en A, on a là un cycle µ1 (fig2)

de deux choses l'une
- si on a utilisé toutes les arêtes du graphe, alors c'est fini (on a de la chance!!)
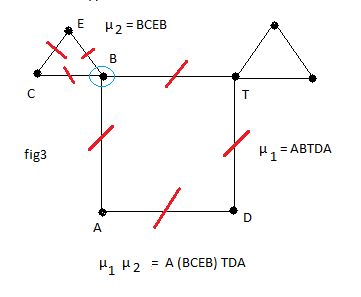
- sinon on prend un sommet B (par exp) de µ1 qui a d'autres arêtes non encore utilisées (fig3) et on recommence , on trouve un autre cycle µ2 à partir de B. Puis on "insère" µ2 dans µ1 en B, c'est-à-dire dans µ1 on remplace B par µ2 (fig3)
µ1 = A(B)TDA
µ2 = BCEB
µ1←µ2 = A(B)TDA ← BCEB = A(BCEB)TDA
On continue .... mais le processus s'arête puisqu'il y a un nombre fini d'arêtes. on trouve donc des cycles µ1,µ2, µ3,... dont on les insère en un seul cycle qui est maintenant eulérien µ
Finalement on trouve un cycle eulérien µ formé par des cycles µ1,µ2,µ3,....(fig4)
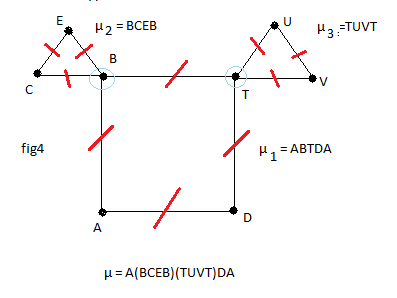
µ1 = A(B)TDA
µ2 = BCEB
µ1←µ2 = A(BCEB)TDA
µ1←µ2 = A(BCEB)(T)DA
µ3 = TUVT
µ = µ1←µ2←µ3 = A(BCEB)(TUVT)DA
Cas 2:
Supposons que dans G il n'y a que deux sommets impairs A et D, il suffit alors de considèrer le graphe G'=G+(A,D), G' a 0 sommet impair, donc il existe un cycle eulérien µ démarrant en A, ainsi dans G on a une chaîne eulérienne entre A et D.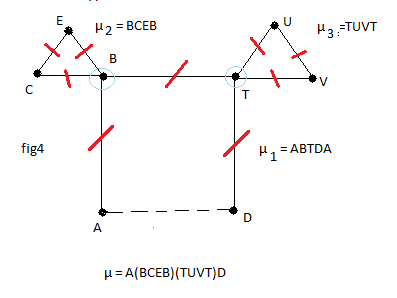
Résumons
Si G (connexe) a 0 inpair ==> cycle eulérien
Si G (connexe) a 2 inpair ==> chaîne eulérienne
1 [2] 3 4
Accueil
DMJ: 23/01/2016