Les triangles
Un triangle ABC c'est un polygone à 3 côtés
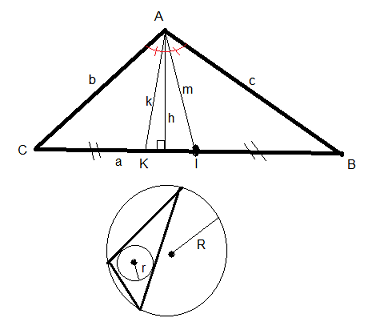
Les données du triangle sont les trois angles : A, B, C et les trois côtés : a, b, c
Et les autres notations
h = hauteur
m = médiane
k = bissectrice
Angles: A, B, C
Côtés: a, b, c
Rayon de cercle circonscrit: R
Rayon de cercle inscrit: r
Surface: S
Demi-perimètre: p = (a+b+c)/2
Voici les relations dans un triangle:
- a² = b² + c² - 2bc cos A (théorème de Pythagore)
- 4m² + a² = 2b² + 2c² (théorème de la médiane)
-
-
-
-
-
-
-
Un triangle est caractérisé par 6 donnés: 3 côtés a, b, c et 3 angles A, B, C si on en donne 3 on peut calculer les autres.
- donnés: a, b, c => on peut trouver A, B, C
- donnés: c, A, b l'angle coincé entre deux côtés => on peut trouver a
- donnés: B, a, C côté coincé entre deux angles => on peut trouver b,c
Les triangles semlables
On dit que deux triangles ABC et A'B'C' sont semlables s' ils ont les même angles par ex: A=A', B=B', C=C'
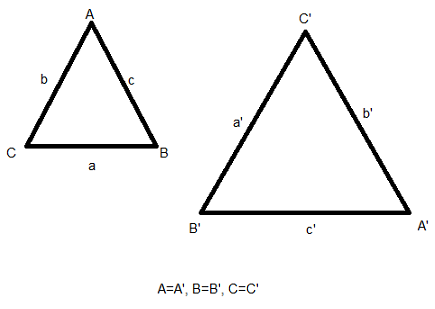
Théorème des triangles semlables : Si deux triangles ABC et A'B'C' sont semlables avec A=A', B=B', C=C' alors on a:
NOTE : Pour avoir les relations entre les côtés on place le 1er triangle puis en dessous le 2ème triangle avec les angles égaux correspondant ex: ABC et PQL semlables
avec A=Q,B=L,C=P
ABC
QLP
AB/QL = BC/LP = AC/QP
Théorème de Céva
Soit ABC un triangle, et A'∈(BC), B'∈(CA) et C'∈(AB) trois points distincts des sommets. Les droites (AA'), (BB') et (CC') sont concourantes ou parallèles si et seulement si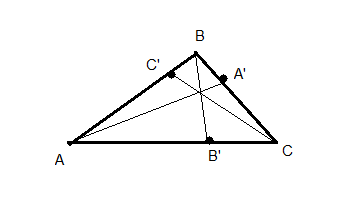 |
|
 |
|
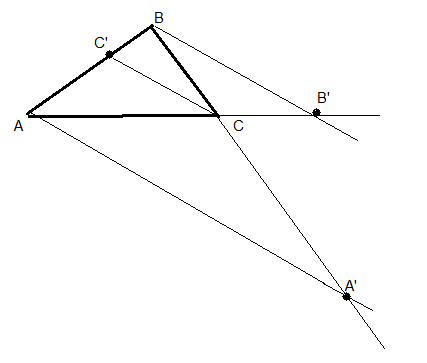
Théorème de Ménélaus
Soit ABC un triangle, et A'∈(BC), B'∈(CA) et C'∈(AB) trois points distincts des sommets. Les points A', B' et C' sont alignés si et seulement si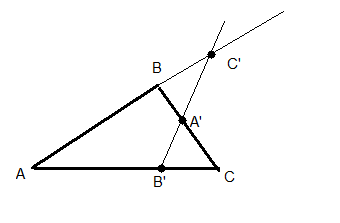 |
|
1 2 3 [4]
Accueil
DMJ: 19/07/2018