On connait mathématiquement assez bien le Pocket , on va faire de même pour le Tori.
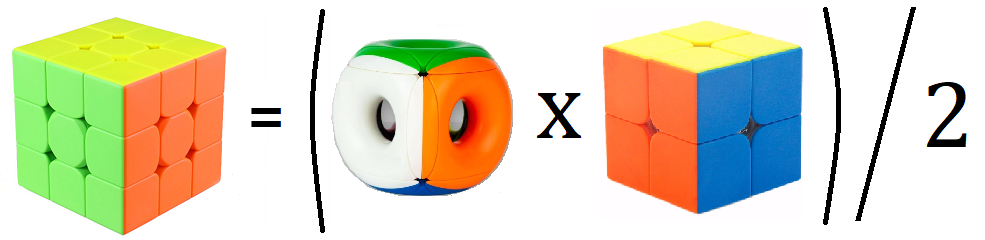
Voici les questions qu'on s'intéresse :
1) Le groupe G du Tori
2) Le nombre d'états (|G|=?)
3) le nombre d'ordre
4) le nombre d'éléments ayant le même ordre d
....
Réponses :
==========
1) On a 12 arêtes qui baladent partout donc on a affaire à S12, et chaque arête a 2 orientations donc on a affaire à Z212
L'ensemble des configurations est donc
G+ = S12 x Z212
On a la loi des flips (F)
(F) x = 0 (mod 2)
La loi (F) donne le nombre de contraintes N=2 (2 choix)
Le groupe de Tori est:
G = G+/N = S12 x Z212 / 2
G = S12 x Z211
2) Le nombre d'états est :|G| = 980995276800
3-4) Avec un programme informatique Jesper C. Gerved et Torben Maack Bisgaard ont trouvé (1981) 32 ordres pour le Tori et le nombre d'états associé.
Voici les 32 ordres triés de rare vers abondant : ordre 2 est rare, ordre 12 est abondants
[ordre, le nbr d'états]
listemoi := [
[ 1, 1 ],
[ 2, 15687871 ],
[ 7, 36495360 ],
[ 3, 95210720 ],
[ 5, 1226548224 ],
[ 15, 1447649280 ],
[ 21, 2919628800 ],
[ 4, 6426894144 ],
[ 120, 8174960640 ],
[ 14, 11350056960 ],
[ 84, 11678515200 ],
[ 70, 14014218240 ],
[ 35, 14014218240 ],
[ 40, 16349921280 ],
[ 56, 17517772800 ],
[ 9, 20437401600 ],
[ 48, 20437401600 ],
[ 36, 27249868800 ],
[ 6, 30243303200 ],
[ 42, 32115916800 ],
[ 28, 36495360000 ],
[ 30, 38745907200 ],
[ 60, 38831063040 ],
[ 16, 40874803200 ],
[ 11, 44590694400 ],
[ 22, 44590694400 ],
[ 8, 54694379520 ],
[ 18, 61312204800 ],
[ 24, 64207503360 ],
[ 10, 64518626304 ],
[ 20, 77355565056 ],
[ 12, 179026805760 ] ] ;;
#Tori = 980995276800



