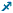Comme tous les cubes de ce genre, on doit connaitre les pièces, leur emplacements et leur
orientations avant de le mélanger, (comme le Golden Cube, Ghost Cube, ....)
Le Skewb Mirror est un SuperSkewb mais la résolution est un peu plus difficile .
En résolvant je suis tombé sur cette singularité-centre : pivoter un centre à 180° !!! (*)

Le twist possède deux centres carrés différents !! il peut donc engendrer des singularité-centre.
Souvenez vous, le Golden Cube-II de Tony possède un centre carré donc lui aussi peut engendrer cette singularité.
Les cubes pouvant engendrer des singularités sont très recherchés, ces singularités donnent le charme de ces cubes.
Voici une formule pour fixer cette singularité:
On tient le cube de telle sorte que:
1) Le centre à pivoter soit à Gauche
2) Un centre carré soit Avant
3) Appliquer doucement la formule : [HE']² [EB']² [O'B]
4 [H'O]
4 = (G)°(A)°
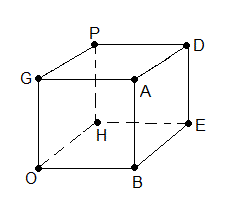
Rotation 120° par rapport aux sommets
(*) NOTE : Pour un Skewb : on ne viole jamais ses lois !! c'est donc il s'agit bien de la "singularité" pas de "problème de parité" , ici il n'y a pas de permutation , il s'agit plutôt l'orientation .
La preuvre que c'est bien une singularité , c'est qu'on obtient cet état par des rotations de base !!!