Commeçons par donner 2 définitions:
Définition 1 : L'ordre d'une formule.
Une formule V est l'ordre d si on a : Vd = I
exemples::
H4 = I ==> H est l'ordre 4,
[DH]6 = I ==> [DH] est l'ordre 6.
Définition 2 : Un quatrix est un nombre entier qui s'écrit avec quatre chiffres '4' et avec les huit oppérations suivantes :
{+, -, x, /, √ , ab, !, 40 }
attention !! entre deux '4' il doit avoir une oppération, donc les écritures '44' , '444' , ... sont interdites
'
23 = 8
5! = 5.4.3.2.1 = 120
40 = 1
exemple:
3 = (4 + 4 + 4)/4
7 = (4 + 4) - (4/4)
.....
Voici la liste des 73 ordres que peut prendre une formule.
LE BUT : exprimer ces ordres en quatrix
1, 2, 3, 4, 5, 6, 7, 8, 9,
10, 11, 12, 14, 15, 16, 18,
20, 21, 22, 24, 28,
30, 33, 35, 36,
40, 42, 44, 45, 48,
55, 56,
60, 63, 66,
70, 72, 77,
80, 84,
90, 99,
105, 110, 112, 120, 126, 132, 140, 144, 154, 165, 168, 180, 198,
210, 231, 240, 252, 280,
315, 330, 336, 360,
420, 462, 495,
504,
630,
720,
840,
990,
1260.
----------
73 ordres
----------
Les ordres des formules et les quatrix
- Morphocode
- Crazy

-

-

- Âge: 100
- Messages : 819
- Inscription : Lun 25/11/2013 17:06
- Localisation : Paris
- Contact :
- Morphocode
- Crazy

-

-

- Âge: 100
- Messages : 819
- Inscription : Lun 25/11/2013 17:06
- Localisation : Paris
- Contact :
Re: Les ordres des formules et les quatrix
J'ai déjà trouvé un certain nombre, mais pas tous ... et je complèterai au fur et à mesure que je trouve.
1 = (4 + 4)/(4 + 4)
2 = (4 + 4) - (4 + √4)
3 = [(4 + 4)+4]/4
4 = [(4 + 4)-√4]-√4
5 = [(4 + 4)+√4]/√4
6 = (4 + 4) - (4 - √4)
7 = (4 + 4) - (4/4)
8 = (4 + 4)(4/4)
9 = (4 + 4) + (4/4)
10 = (4 + 4) + (4 - √4)
11 = [(√4 + 4!)-4]/√4
12 = [(4 + 4)+√4]+√4
14 = (4 + 4) + (4 + √4)
15 = [(4 + √4)+4!]/√4
16 = (4 + 4) + (4 + 4)
18 = (4 + √4) + (4!/√4)
20 = (4 + 4) + (4!/√4)
21 = 4! - 4 + 4/4
22 = (4 + √4) + (4x4)
24 = (4 + 4) + (4x4)
28 = (4 + 4) + (4! - 4)
30 = (4 + 4) + (4! - √4)
33 = [√√(√44!)+√4]/√4
35 = [(4! - √4)/√4]+4!
36 = (4 + 4) + (4 + 4!)
40 = [(4 + 4)+√4]4
42 = (4x4) + (√4 + 4!)
44 = (4 + 4!) + (4x4)
45 = [√4-√√√(√4-4!)]4!
48 = (4 + 4)(4 + √4)
1 = (4 + 4)/(4 + 4)
2 = (4 + 4) - (4 + √4)
3 = [(4 + 4)+4]/4
4 = [(4 + 4)-√4]-√4
5 = [(4 + 4)+√4]/√4
6 = (4 + 4) - (4 - √4)
7 = (4 + 4) - (4/4)
8 = (4 + 4)(4/4)
9 = (4 + 4) + (4/4)
10 = (4 + 4) + (4 - √4)
11 = [(√4 + 4!)-4]/√4
12 = [(4 + 4)+√4]+√4
14 = (4 + 4) + (4 + √4)
15 = [(4 + √4)+4!]/√4
16 = (4 + 4) + (4 + 4)
18 = (4 + √4) + (4!/√4)
20 = (4 + 4) + (4!/√4)
21 = 4! - 4 + 4/4
22 = (4 + √4) + (4x4)
24 = (4 + 4) + (4x4)
28 = (4 + 4) + (4! - 4)
30 = (4 + 4) + (4! - √4)
33 = [√√(√44!)+√4]/√4
35 = [(4! - √4)/√4]+4!
36 = (4 + 4) + (4 + 4!)
40 = [(4 + 4)+√4]4
42 = (4x4) + (√4 + 4!)
44 = (4 + 4!) + (4x4)
45 = [√4-√√√(√4-4!)]4!
48 = (4 + 4)(4 + √4)

- Morphocode
- Crazy

-

-

- Âge: 100
- Messages : 819
- Inscription : Lun 25/11/2013 17:06
- Localisation : Paris
- Contact :
Re: Les ordres des formules et les quatrix
55 = [(4 + 4!)√4] - 40
56 = (4 + 4) + (√4x4!)
60 = [(4 + 4)√4] - 4
63 = √√(√44!) - (4/4)
66 = (4 - √4) + √√(√44!)
70 = (4 + √4) + √√(√44!)
72 = (4 + 4) + √√(√44!)
77 = [(4 - 40)^4] - 4
80 = [(4 + 4!)√4] + 4!
84 = [(4! - 4)4]+4
90 = (4x4!) - (4 + √4)
99 = [4+√√√(√4-4!)]4!
56 = (4 + 4) + (√4x4!)
60 = [(4 + 4)√4] - 4
63 = √√(√44!) - (4/4)
66 = (4 - √4) + √√(√44!)
70 = (4 + √4) + √√(√44!)
72 = (4 + 4) + √√(√44!)
77 = [(4 - 40)^4] - 4
80 = [(4 + 4!)√4] + 4!
84 = [(4! - 4)4]+4
90 = (4x4!) - (4 + √4)
99 = [4+√√√(√4-4!)]4!

- Morphocode
- Crazy

-

-

- Âge: 100
- Messages : 819
- Inscription : Lun 25/11/2013 17:06
- Localisation : Paris
- Contact :
Re: Les ordres des formules et les quatrix
105 = [(4 - 40)^4] + 4!
110 = 4(4!+4) - √4
112 = 4x4! + 4x4
120 = (√4+√4 + 4/4)!
126 = (44/√4) - √4
132 = (4 + √4)(4! - √4)
140 = [(4 + √4)4!] - 4
144 = 4x4! + 4! + 4!
168 = [(4 + √4)4!] + 4!
180 = (√4+√4+√4)!/4
210 = [(4!+4)/4]!/4!
231 = (4^4) - (4! + 40)
240 = 44 - 4x4
252 = 44 - √4 - √4
280 = 44 + (√4 + √4)!
336 = (4 + 4!)(4!/√4)
360 = [(4x4)4!] - 4!
462 = (4! - √4)! / (4! - 4)!
504 = (44 - 4)√4
720 = (√4 + √4 + 4/√4)!
840 = (4+4)! / (4!+4!)
1260 = [(4!+4)/4]!/4 ===> il vraiment étonnant que l'ordre maximal est un quatrix !!!
Il nous reste 8 à trouver: 165, 198, 315, 330, 420, 495, 630, 990.

110 = 4(4!+4) - √4
112 = 4x4! + 4x4
120 = (√4+√4 + 4/4)!
126 = (44/√4) - √4
132 = (4 + √4)(4! - √4)
140 = [(4 + √4)4!] - 4
144 = 4x4! + 4! + 4!
168 = [(4 + √4)4!] + 4!
180 = (√4+√4+√4)!/4
210 = [(4!+4)/4]!/4!
231 = (4^4) - (4! + 40)
240 = 44 - 4x4
252 = 44 - √4 - √4
280 = 44 + (√4 + √4)!
336 = (4 + 4!)(4!/√4)
360 = [(4x4)4!] - 4!
462 = (4! - √4)! / (4! - 4)!
504 = (44 - 4)√4
720 = (√4 + √4 + 4/√4)!
840 = (4+4)! / (4!+4!)
1260 = [(4!+4)/4]!/4 ===> il vraiment étonnant que l'ordre maximal est un quatrix !!!
Il nous reste 8 à trouver: 165, 198, 315, 330, 420, 495, 630, 990.

- Morphocode
- Crazy

-

-

- Âge: 100
- Messages : 819
- Inscription : Lun 25/11/2013 17:06
- Localisation : Paris
- Contact :
Re: Les ordres des formules et les quatrix
Un complément sur les quatrix
Rappel la définition :
Un quatrix est un nombre qui s'écrit avec quatre chiffres '4' et les 8 opérations suivantes E = { +, -, x, /, √, ab, !, 40 }
Rappel
√4 = 2
23 = 2x2x2 = 8
5! = 5x4x3x2x1 = 120
40 = 1
NOTE:
-Les parenthèses '(', ')' et les crochets '[', ']'' sont autorisées , c'est juste pour la visibilité des lectures.
-Les écritures 44, 444, 4444, ... ne sont pas autorisées.
Justification de l'opération 40 :
Les opérations { +, -, x, ab, ! } applique sur le chiffre '4' donne un nombre pair , ce qui fait que pour former un nombre impair est plutôt dificile 2/7 de chance, c'est pour équiliber cette chance on veut ajouter une 8ème opération qui forme le 1 avec un seul '4'.
Il y a plusieurs candidatures:
1) [x] partie entière de x : ==> [√√4] = 1
2) Γ(n) = (n-1)! la fonction gamma : ==> Γ(√4) = (2-1)! = 1! = 1
... etc ....
Pour nous c'est simplement 40 = 1
Justification:
on a
√√√4 = (4)1/(2^3)
√√... √√√4 = (4)1/(2^n) ; il y a n '√'
donc à la limite on aura:
... √√√4 = (4)0 ; puisque 1/(2^n) tend vers zéro 0 quand n tend vers ∞
On pose: ...√√√4 = 40 , donc 40 est une sorte de limite , une suite infinie d'opération √
On a une formule très étonnante, tout entier n s'exprime avec quartre '4' et le 'log' !!
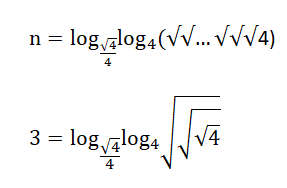
où √√... √√√ = n '√' (n racines carrées)
Il est remarquable que i, π et ϕ (nombre d'or) sont des quatrix !! en effet
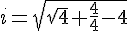
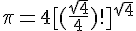
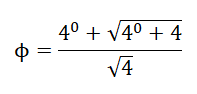
Vous trouverez un javasript pour les quatrix .::ICI::.
https://fan2cube.fr/mathsotop/quatrix/quatrix.js
https://fan2cube.fr/mathsotop/quatrix/quatrix.html
Rappel la définition :
Un quatrix est un nombre qui s'écrit avec quatre chiffres '4' et les 8 opérations suivantes E = { +, -, x, /, √, ab, !, 40 }
Rappel
√4 = 2
23 = 2x2x2 = 8
5! = 5x4x3x2x1 = 120
40 = 1
NOTE:
-Les parenthèses '(', ')' et les crochets '[', ']'' sont autorisées , c'est juste pour la visibilité des lectures.
-Les écritures 44, 444, 4444, ... ne sont pas autorisées.
Justification de l'opération 40 :
Les opérations { +, -, x, ab, ! } applique sur le chiffre '4' donne un nombre pair , ce qui fait que pour former un nombre impair est plutôt dificile 2/7 de chance, c'est pour équiliber cette chance on veut ajouter une 8ème opération qui forme le 1 avec un seul '4'.
Il y a plusieurs candidatures:
1) [x] partie entière de x : ==> [√√4] = 1
2) Γ(n) = (n-1)! la fonction gamma : ==> Γ(√4) = (2-1)! = 1! = 1
... etc ....
Pour nous c'est simplement 40 = 1
Justification:
on a
√√√4 = (4)1/(2^3)
√√... √√√4 = (4)1/(2^n) ; il y a n '√'
donc à la limite on aura:
... √√√4 = (4)0 ; puisque 1/(2^n) tend vers zéro 0 quand n tend vers ∞
On pose: ...√√√4 = 40 , donc 40 est une sorte de limite , une suite infinie d'opération √
On a une formule très étonnante, tout entier n s'exprime avec quartre '4' et le 'log' !!
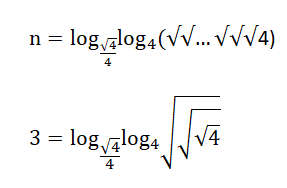
où √√... √√√ = n '√' (n racines carrées)
Il est remarquable que i, π et ϕ (nombre d'or) sont des quatrix !! en effet
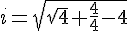
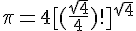
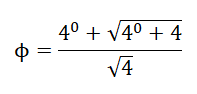
Vous trouverez un javasript pour les quatrix .::ICI::.
https://fan2cube.fr/mathsotop/quatrix/quatrix.js
https://fan2cube.fr/mathsotop/quatrix/quatrix.html
