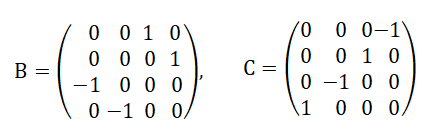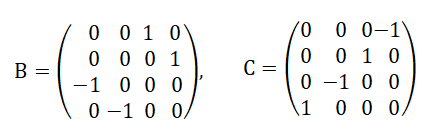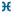Matrice et état

[Morphocode]

Voici deux matrices B et C ci-dessous

Si on vous demande de représenter la matrice B par un état (motif) du Rubik's Cube quel état (motif) proposez vous ?
Même question pour la matrice C .

[TomCube]

Très bonne question, je serai très intéressé par la réponse

[Morphocode]

Solution:
Si on observe bien, la matrice B comporte quatre blocs de 2x2, les deux blocs zéro ça ne sert à rien ! il nous reste deux blocs donc 8 éléments, chaqu' élément prend les valeurs 0,1,-1 et leur somme vaut zéro, ceci nous fait penser aux 8 sommets du Rubik's Cube et leurs 3 orientations 0(bien orienté), 1(dans le sens horaire) et -1(sens anti-horaire).



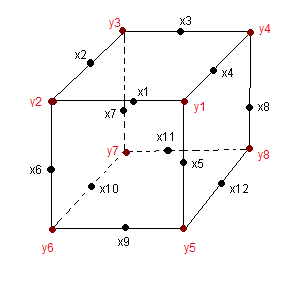
Autrement dit on peut représenter la matice B par le vecteur d'orientation y=(y1,y2,y3,y4,y5,y6,y7,y8) des sommets.
il suffit de nommer les 8 éléments de la matrice comme ceci


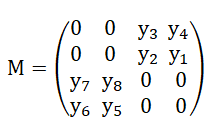
avec yi=0,1,-1 et Σyi=0 (mod 3)


l'état correspond à la matrice B est donc :

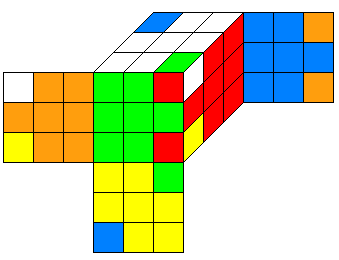
b=(id,0,id,y) avec y=(1,0,1,0,-1,0,-1,0)

De même pour la matrice C, l'état correspond à la matrice C est :

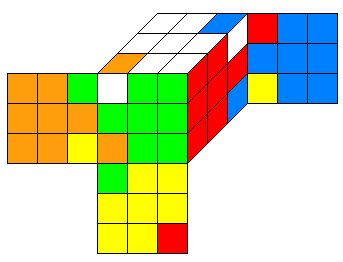
c=(id,0,id,y) avec y=(0,1,0,-1,0,1,0,-1)

REMARQUE IMPORTANTE :
- L'état b représente la matrice B et la matrice B représente le quaternion j, mais l'état b ne représente pas le quaternion j !!! le quaternion j est représenté par l'état :
j = (u,x,id,0) où u=(1,2)(3,4) et x=(1,0,0,1,0,0,0,0,0,0,0,0)

- L'état c représente la matrice C et la matrice C représente le quaternion k, mais l'état c ne représente pas le quaternion k !!! le quaternion k est représenté par l'état :
k = (u,x,id,0) où u=(1,3)(2,4) et x=(0,0,1,1,0,0,0,0,0,0,0,0)