Une des façons de s'en sortir est:
1) Ranger toutes les arêtes.
2) Ranger tous les sommets.
Supposons qu'on a rangé toutes les arêtes , voici quelques formules pour ranger les sommets.
Les formules sont valables dans la position CONTROLE ci-dessous
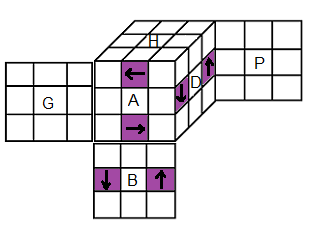
Pour trouver les formules on utilise les K-formule !
Rappelle : Une K-formule est une formule qui n'échange ou pivote qu'une seule picèce de la face K.
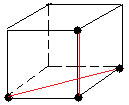
1) Voyons la formule
[DA'] = DA'D'A
qui échange une seule pièce Haut (HDA)
donc on peut fabriquer un 3-cycle-sommet , il suffit de prendre:
[[DA'],H'] = [DA'] H'[A'D]H = (HDA)->(HAG)->(BAD)
De même la formule
[DA']² = (DA'D'A)²
pivote une seule pièce Haut (HDA)
donc on peut pivoter 2 sommets , il suffit de prendre:
[[DA']²,H'] = [DA']² H'[A'D]²H = (HDA)
+(HAG)
-2) On peut dire aussi que la formule
[DA'] = DA'D'A
échange une seule pièce Gauche (BGA)
donc on peut fabriquer un 3-cycle-sommet , il suffit de prendre:
[[DA'],G'] = [DA'] G'[A'D]G = (BGA)->(BPG)->(BDP)
De même la formule
[DA']² = (DA'D'A)²
qui pivote une seule pièce Gauche (BGA)
donc on peut pivoter 2 sommets , il suffit de prendre:
[[DA']²,G'] = [DA']² G'[A'D]²G = (BGA)
-(BPG)
+3) On peut dire aussi que la formule
[DA'] = DA'D'A
échange une seule pièce Postérieur (BDP)
donc on peut fabriquer un 3-cycle-sommet , il suffit de prendre:
[[DA'],P'] = [DA'] P'[A'D]P = (BDP)->(HPD)->(BGA)
De même la formule
[DA']² = (DA'D'A)²
qui pivote une seule pièce Postérieur (BDP)
donc on peut pivoter 2 sommets , il suffit de prendre:
[[DA']²,P'] = [DA']² P'[A'D]²P = (BDP)
-(HPD)
+* On pourrait faire la même chose avec la formule [D'H']
_________________________________________________
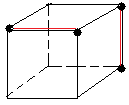
1) La formule
[D'H'] = D'H'DH
échange une seule pièce Gauche (HAG)
donc on peut fabriquer un 3-cycle-sommet , il suffit de prendre:
[[D'H'],G] = [D'H'] G[H'D']G' = (HAG)->(HDA)->(HGP)
De même la formule
[D'H']² = (D'H'DH)²
pivote une seule pièce Haut (HAG)
donc on peut pivoter 2 sommets , il suffit de prendre:
[[D'H']²,G] = [D'H']² G[H'D']²D' = (HAG)
+(HGP)
-2) On peut dire aussi que la formule
[D'H'] = D'H'DH
échange une seule pièce Bas (BDP)
donc on peut fabriquer un 3-cycle-sommet , il suffit de prendre:
[[D'H'],B] = [D'H'] B[H'D']B' = (BDP)->(BAD)->(HPD)
De même la formule
[D'H']² = (D'H'DH)²
pivote une seule pièce Gauche (BDP)
donc on peut pivoter 2 sommets , il suffit de prendre:
[[D'H']²,B] = [D'H']² B[H'D']²B' = (BDP)
-(BAD)
+






