l'exploration du graphe (d'états) T du Twist. En générale ce graphe
est trop gros, on voudrait réduire ce graphe à un autre graphe Q de taille plus petit
pour faciliter l'exploitation.
Jerry BRYAN a eu l'idée de classer les états suivant un certain critère nommé "J-conjugaison"
où J est le groupe d'isométrie du Twist.
le graphe Q "J-conjugaison" est environ |J| fois plus petit que T donc l'exploration est plus vite.
La donnée d'un état s=e•V , V∈M est équivalente à la donnée la permutation pV donc travailler
sur G c'est la même chose de travailler sur Λ, dans cet article on va travailler dans Λ.
Les classes J-conjugaison du Pyraminx:
------------------------------------------------
On sait que J est inclus dans S24 grâce au théorème : K un goupe fini alors K est isomorphe à un sous groupe S|K|,
autrement dit K ⊂ dans S|K|.
J ⊂ S24 ⊂ S36 (36 autocollants)
Λ est aussi inclus dans S36
On va définir une relation d'équivalence sur Λ de la façon suivante:
Λ = < pG, pD, pH, pP, pg, pd, ph, pp >
p,q ∈Λ
p~q <=> ∃f∈J tel que fpf-1 = q ; p,q,f ∈S36 donc la déf a un sens
et les classes d'équivalence de cette relation nommées les classes J-conjugaison
Le nombre de classes w est donné par la formule de Burnside :
w = 1/|J| Σ |Ff| ; sommer sur (f ∈J)
Ff = {p ∈ Λ | fpf-1 = p}
Ff = {p ∈ Λ | fp = pf}
Les calculs se font en GAP.
1. On sait paramétrer le Twist en GAP càd trouver Λ
2. La plus grande difficulté c'est de convertir J en GAP càd trouver
J = < a,b,c, ...> où a,b,c, ... permutations de S36
On ignore les orientations donc les sommets sont repérés par un seul nombre
pour nous c'est : 28,31,25,34 (d'après les numérotations des autocollants)
or on sait que J=S4 et
S4 = < (28,31),(28,31,25,34) >
Voici un script en GAP qui calcule le nombre w de classes de J-conjugaison.
On calcule w en GAP :
Code : Tout sélectionner
#Les données du Pyraminx en GAP
#permutation sommet
pG := (28,29,30);
pD := (31,32,33);
pH := (25,26,27);
pP := (34,36,35);
#per tranche: (arete)(arete)(centre)
pg := (2,4,11)(8,10,5)(21,15,16);
pd := (1,12,4)(7,6,10)(17,14,24);
ph := (1,8,9)(7,2,3)(22,13,20);
pp := (3,5,12)(9,11,6)(23,19,18);
#per-croisée
pGs := (1,3,6)(7,9,12)(13,19,17)(14,20,18)(22,23,24)(25,34,33)(26,36,31)(27,35,32);
pDs := (2,5,9)(3,8,11)(13,16,23)(15,18,22)(19,20,21)(25,29,35)(26,30,34)(27,28,36);
pHs := (4,6,5)(10,12,11)(14,23,21)(15,24,19)(16,17,18)(28,32,34)(29,33,36)(30,31,35);
pPs := (1,2,10)(4,7,8)(13,15,14)(16,24,20)(17,22,21)(25,28,31)(26,29,32)(27,30,33);
#permutations étendues (violer les lois)
pGamma := (1,7);
pOmega := (1,2)(7,8);
Pyraminx := Group( pG, pD, pH, pP, pg, pd, ph, pp);
###Iso=S4
j1 := (28,31);
j2 := (28,31,25,34);
Iso := Group (j1,j2) ;
#IsSubgroup(Pyraminx, Iso) ;
#StructureDescription(Iso) ;
#NrConjugacyClasses( Iso ) ;
#Clcjg := ConjugacyClasses(Iso); # les classes de conjugaisons
#Size(Clcjg[2]);
#List(Clcjg[2]);
###Dep=A4
d1:=(25,28)(31,34) ;
d2:=(25,31)(28,34);
d3:= (25,34,31) ;
Dep := Group( d1,d2,d3 ) ;
#####
G := Pyraminx ;;
Gtxt := "Pyraminx" ;;
J := Iso ;;
Jtxt := "J" ;;
############
Clcjg := ConjugacyClasses( J ) ;;
h := NrConjugacyClasses( J ) ;;
w := 0;
Print("\n\n Type-Iso \t Pt-fixe\n" );
Print("================================= \n" );
for i in [1..h] do
q := Representative(Clcjg[i]); #prendre un représentant de la classe ==> q
zz := Size( Centralizer(G,q) ) ; #le nombre de pt fixe engendré par q
zz := zz * Size(Clcjg[i]) ; #le nombre de pt fixe engendré par Clcjg[i]
Print("\n",i,") ",zz,"\n");
w := w + zz ; #accumulation
od;
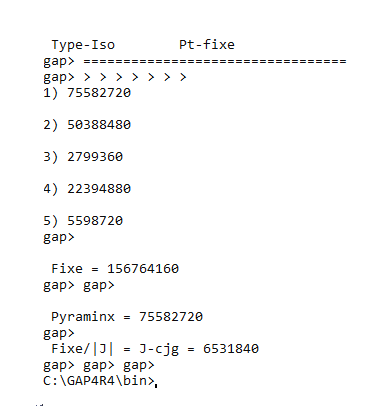
Print("\n\n Fixe = ", w, "\n" );
w := w/Size(J) ;; #le nbr de classes
Print("\n\n ",Gtxt," = ", Size(G), "\n" );
Print("\n Fixe/|J| = ",Jtxt,"-cjg = ", w , "\n" );