Fan2Cube

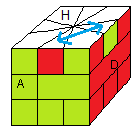
l'état µ

Lorsqu'on manipule le Square-1 tôt ou tard on rencontre cet état µ
c'est un état qu'on nomme le "problème de parité" .
Q1) Pourquoi cet état µ pose un problème ?
Q2) Pourquoi c'est un problème de parité ?
Q3) Quelle est la cause ?
Q4) Quelle est la probabilité d'avoir cet état µ ?

Pour bien comprendre cet état et répondre à ces questions, on s'appuies sur le Super Floppy.
Le Super Floppy bien que c'est un très simple twist, mais il se comporte exactement comme le Square-1

===============
Super Floppy:
Les rotations de base : {H²,B²,G²,D²}
Les rotations étendues : H,B,G,D, arête_90°, arête_sommet_90°
Loi de parité : sig(sommets) = (-1)k ; k=nombre de flips (des arêtes)


Quand on mélange le Twist uniquement par des rotations de base, le Twist garde la forme carrée, plat et vérifie la loi de parité càd
les sommets et les arêtes sont "en phase" .
Mais si le mélange comporte des rotations étendues le Twist change de forme.
Lorsqu'on arrive à la forme carrée peut-être, les sommets et les arêtes ne sont plus en phase
Dans ce cas, cet état µ viole la loi de parité et à la fin de la résolution on aura le problème de parité.

Pour fixer la parité, il faut utiliser les rotations étendues .


Le mélange comporte des rotations étendues le Twist change de forme.


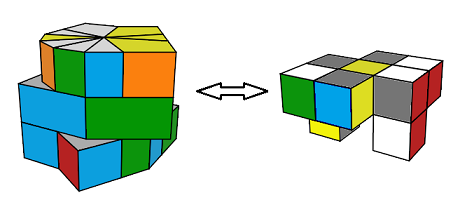
forme cubique, forme carrée.


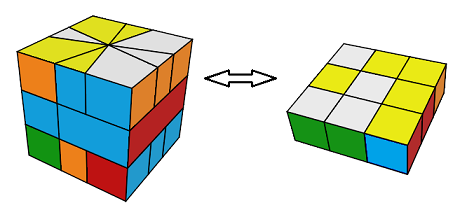
l'état de parité µ


===================
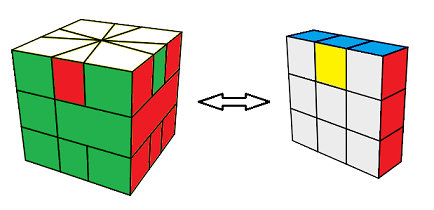
C'est exactement la même chose pour le Square-1, sauf les rotations de base sont plus compliquées
et la loi de parité est différente.

Square-1 :
On pose:
S = 1/3/-1 , Q = 1/3B/-1
E = -B/3/B , T = -B/3B/B
Les rotations de base : {3, 3B, S, Q, E, T}
Les rotations étendues : 1, B, /
Loi de parité : sig(sommets) = sig(arêtes)

Quand on mélange le Twist uniquement par des rotations de base, le Twist garde la forme cubique et vérifie la loi de parité.


R1) Cet état µ pose un problème, car il viole une loi du Twist
R2) Parce que cet état viole la loi de parité ==> sig(sommets) ≠ sig(arêtes)
R3) Parce que le mélange contient au moins une rotation étendue
R4) La probabilité d'avoir le problème de parité est : 1/2