Fan2Cube

on l' achète ICI
https://www.cubezz.com/Buy-4137-DianSheng+Shield+Magic+Cube+White.html


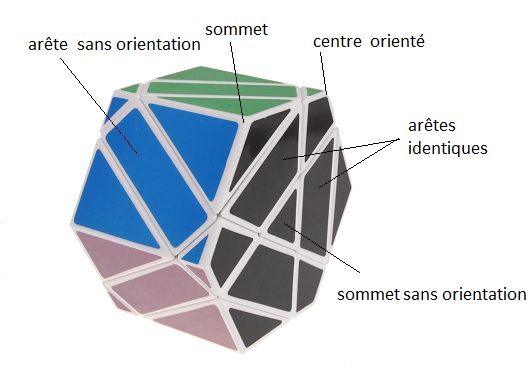
Pour bien comprendre la singularité d'un super 3x3x3, on va observer le twist ci-dessus .
Mais avant rappellons les 4 lois d'un super 3x3x3 :
1) Loi des flips : la somme des orientations des arêtes est un multiple de 2
2) Loi des twists : la somme des orientations des sommets est un multiple de 3
3) Loi de parité : les sommes et les arêtes sont en phase : sig(sommets) = sig(arêtes)
4) Loi des centres : la somme des rotations (à 90°) des centres est un multiple de 2

*Ce Cube possède des arêtes sans orientation ==> ceci gènère la singulatité-arête-orientation :
pivoter une seule arête : on pivote une arête sans orientation avec une arête à 2 orientations

*Ce Cube possède 2 sommets sans orientation ==> ceci gènère la singulatité-sommet-orientation :
pivoter un seul sommet: on pivote un sommet sans orientation avec un sommet à 3 orientations

*Ce Cube possède des arêtes identiques ==> ceci gènère la singulatité-sommets :
permuter 2 sommets : on permute un couple d'arêtes identiques et un couple sommets

Les états singuliers sont des états l'égaux
Les états singuliers vérifient les lois donc il n'y a pas de "problème" (problème de parité) !!!