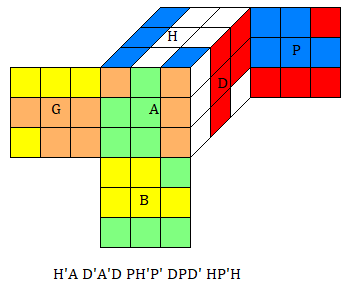
On pose:
b = le nombre de blanc d'une face
j = le nombre de jaune d'une face
v = le nombre de vert d'une face
k = le nombre de klein d'une face
o = le nombre d' orange d'une face
r = le nombre de rouge d'une face
La chromatique de la face Haut
H = b²+j²+v²+k²+o²+r²
et la chromatique de l'état s
X = H+B+A+P+G+D
par ex:
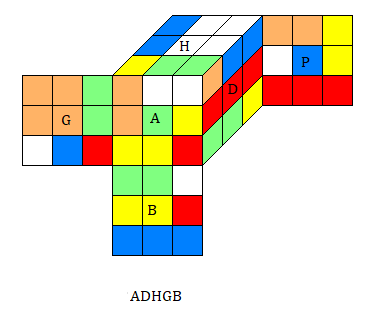
H = 4²+2²+2²+1² = 25
B = 3²+2²+2²+1²+1² = 19
A = 3²+2²+2²+1²+1² = 19
P = 3²+2²+2²+1²+1² = 19
G = 4²+2²+1²+1²+1² = 23
D = 3²+2²+2²+1²+1² = 19
X = 124
Le maximum de la chromatique d'une face est 81, quand la face a une seule couleur.
Le minimum de la chromatique d'une face est 15, quand la face possède 6 couleurs et aucune apparait
plus de 3 fois càd (2²+2²+2²+1²+1²+1²)
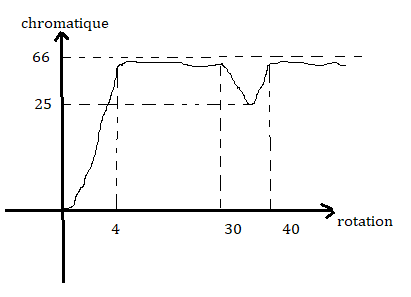
Lorsqu'on mélange le Cube au hasard , le graphe montre que la chromatique X est minium=90 en quelques rotations
et elle oscille autour de cette valeur. Puis de 30-40 rotations X monte à 131, et au-delà de 40 rotations elle descend à 99 ⩽ s
pour X = 81 x 6 = 486, on a un seul état, l'état résolu e
pour X = 342, on a 12 états (une rotation A,B, ..., A',B', ...)
pour un X donné , il se peut qu'il y ait beaucoup d' états correspondants.
Le but : On cherche des états dont chaque face a la même motif et H=B=A=P=G=D .
par ex:
V = H'AD'A'DPH'P'DPD'HP'H (motif "pd")
H = B = ... = 5²+4² = 41 (même motif)