et on le résout uniquement avec ces deux rotations H et D.
Une chose curieuse s'est produit:
Quand les deux sommet Bas (BDP) et (BAD) sont bien placés alors, les 4 sommets Haut sont automatiquement bien placés aussi !!
(quitte à faire des rotations H si nécessaire). Autrement dit on place le sommet Haut (HDA) avec la rotation H,
Les trois autres sommets Haut sont automatiquement bien placés !
1) Pourquoi on ne peut pas avoir 3 sommets Haut mal placés, quand les deux sommets Bas sont bien placés ?
2) De même pourquoi on ne peut pas avoir 2 sommets Haut mal placés, quand les deux sommets Bas sont bien placés ?
On peut utiliser GAP pour avoir la réponse:
On numérote les 6 sommets comme indique la fig ci-dessous
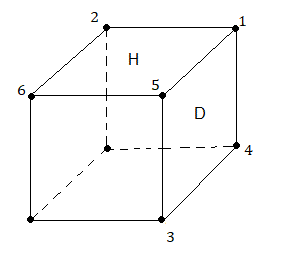
La rotation H donne la permutation pH=(1,5,6,2) et la rotation D donne la permutation pD=(1,4,3,5)
G = <pH, pD>
l'élément a=(6,2,1) par ex n'appartient pas à G,
de même l'élément b=(6,2) par ex n'appartient pas non plus à G,
ça signifie que ces deux configurations sont impossibles à atteindre donc on ne peut pas avoir un 3-cycle
ou un 2-cycle de sommets Haut quand les autres sommets sont fixes.
Code en GAP
Code : Tout sélectionner
G := Group((1,5,6,2),(1,4,3,5));
Size(G);
a := Group((6,2,1));
b := Group((2,6));
IsSubgroup( G, a );
IsSubgroup( G, b );
List(G) ;
On voit il n'y a pas de 3-cycle ni de 2-cycle




