Les singularités chez le Void Cube
Publié : Ven 17/11/2023 17:53
Sur le Net, sur Youtube, dans les Forums ... et les algorithmes de résolution du Void Cube désignent les deux états ci-dessous comme des états qui posent des problèmes : le "problème de parité" .
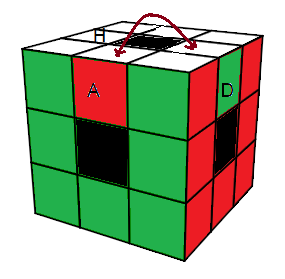
état (a)
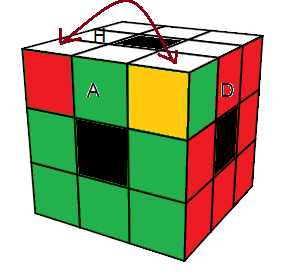
état (b)
Les rotations de base : {H, h, a, P, G, D}
Les sommets et les arêtes sont orientés comme en Rubik's Cube,
Voici les lois du Void Cube :
(F) L'orientation des arêtes est un multiple de 2 (x=0 (mod 2) )
(T) L'orientation des sommets est un multiple de 3 (y=0 (mod 3) )
Il n'y a pas de loi de parité chez le Void Cube !!
Ces 2 états ne violent aucune loi, ce sont des états légaux, la preuve c'est qu'ils
proviennent des rotations de base.
(a) = HD²H'aH . D²H²aHa'
(b) = HD'G'H² GHG' H²DH'G . HD²H'aH . D²H²aHa'
L'état (a) s'appelle singularité-arêtes
L'état (b) s'appelle singularité-sommets

état (a)

état (b)
Les rotations de base : {H, h, a, P, G, D}
Les sommets et les arêtes sont orientés comme en Rubik's Cube,
Voici les lois du Void Cube :
(F) L'orientation des arêtes est un multiple de 2 (x=0 (mod 2) )
(T) L'orientation des sommets est un multiple de 3 (y=0 (mod 3) )
Il n'y a pas de loi de parité chez le Void Cube !!
Ces 2 états ne violent aucune loi, ce sont des états légaux, la preuve c'est qu'ils
proviennent des rotations de base.
(a) = HD²H'aH . D²H²aHa'
(b) = HD'G'H² GHG' H²DH'G . HD²H'aH . D²H²aHa'
L'état (a) s'appelle singularité-arêtes
L'état (b) s'appelle singularité-sommets
Donc parler de problème de parité n'a pas de sens chez le Void Cube !