Le nombre d'états d'un Cube
Publié : Jeu 6/01/2022 12:05
Un état est une configuration (des autocollants) provenant des rotations de base en respectant l'orientation du Cube (pas bouger, pas tourner le Cube) , de plus si le Cube a des pièces indiscernables (comme le Revenge, Professor, V-Cube, ...) alors les états doivent être visuellement distingues.
Donc avant de parler le nombre d'états d'un Cube, il faut fixer le Cube (orienter le Cube), traditionnellement on fixe le Cube ainsi :
Haut=blanc, Bas=jaune, Avant=vert, Postérieur=klein, Gauche=orange, Droite=rouge
ET préciser quels sont les rotations standards (les rotations de base)
Les configurations provenant des rotations standards se nomment les états du Cube.
Par ex
=> pour l'Helicopter les rotations standards sont les 12 rotations d'arêtes à 180°, les autres rotations sont non-standards
=> pour le Rubik's Cube les rotations standards sont {H,B,A,P,G,D} , les autres rotations tranches h,d,a ... sont non-standards
Quand on parle d'états du Rubik's Cube ce sont des états provenant des rotations de base {H,B,A,P,G,D}.
=> Pour le Skewb , les rotations standards sont les 8 rotations sommets à 120°.
Exemples :
==========
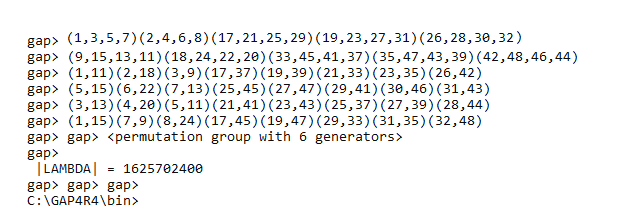
Le nombre d'états du Rubik's Cube
=============================
Pour calculer le nombre d'états du Rubik's Cube on suit la recette suivante:
Pour le Rubik's Cube:
=> On a 12 arêtes qui baladent partout en restant dans leur camp, donc le nombre de permutations est 12! (à connaitre par coeur)
=> Chaqu' arête a 2 orientations, donc le nombre d'orientations est 212 (à connaitre par coeur)
=> On a 8 sommets qui baladent partout en restant dans leur camp, donc le nombre de permutations est 8!
=> Chaque sommet a 3 orientations, donc le nombre d'orientations est 38
donc le nombre de configurations est :
12!.212 x 8!.38
Mais on a des contraintes (des lois), pour avoir le nombre d'états il faut donc diviser le nombre de configurations par les contraintes:
=> loi des flips => /2 (car on a 2 choix)
=> loi des twists => /3 (car on a 3 choix)
=> loi de parité => /2 (car on a 2 choix)
Finalement le nombre d'états du Rubik's Cube vaut:
g = 12!.212 x 8!.38 /2.3.2


==========
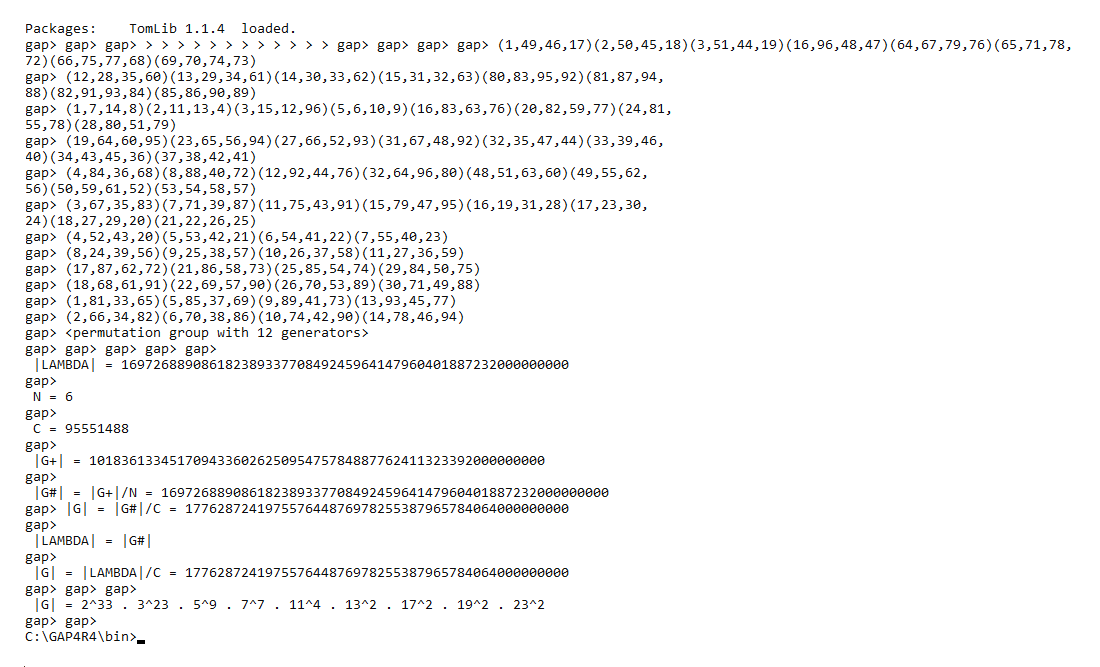
Le nombre d'états du Revenge
=============================
Pour calculer le nombre d'états du Revenge on suit la recette suivante:
Pour le Revenge:
=> On a 8 sommets qui baladent partout en restant dans leur camp, donc le nombre de permutations est 8!
=> Chaque sommet a 3 orientations, donc le nombre d'orientations est 38
=> On a 24 ailes qui baladent partout en restant dans leur camp, donc le nombre de permutations est 24! (à connaitre par coeur)
=> On a 24 centres qui baladent partout en restant dans leur camp, donc le nombre de permutations est 24!
donc le nombre de configurations est :
8!.38 x 24! x 24!
Mais on a des contraintes (des lois), pour avoir le nombre d'états il faut donc diviser le nombre de configurations par les contraintes:
=> loi des twists => /3 (car on a 3 choix)
=> loi de parité (sommets et centres en phase) => /2 (car on a 2 choix)
=> visuellement identique => /(4!6/2) (le nombre permutations des centres)
Finalement le nombre d'états du Revenge vaut:
g = 8!.38 x 24! x 24! /3 .2 . (4!6/2)
g = 8!.37 x (24!)² / 4!6


Le nombre d'états du Skewb
=========================
Les sommets du Skewb sont divisés en deux camps : le camp Impair et le camp Pair
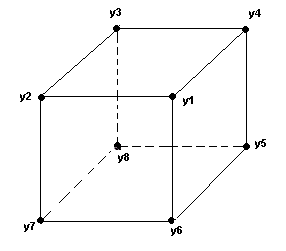
Pour le Skewb:
=> On a 4 sommets Impairs qui baladent partout dans son camp, donc le nombre de permutations est 4! (à connaitre par coeur)
=> Chaque sommet Impair a 3 orientations, donc le nombre d'orientations est 34 (à connaitre par coeur)
=> On a 4 sommets Pairs qui baladent partout dans son camp, donc le nombre de permutations est 4! (à connaitre par coeur)
=> Chaque sommet Pair a 3 orientations, donc le nombre d'orientations est 34 (à connaitre par coeur)
=> On a 6 centres qui baladent partout en restant dans leur camp, donc le nombre de permutations est 6!
donc le nombre de configurations est :
4!.34 x 4!.34 x 6!
Mais on a des contraintes (des lois), pour avoir le nombre d'états il faut donc diviser le nombre de configurations par les contraintes:
=> loi des twists pour les sommets Impairs => /3 (car on a 3 choix)
=> loi des twists pour les sommets Pairs => /3 (car on a 3 choix)
=> loi de parité pour les sommets Impairs => /2 (car on a 2 choix)
=> loi de parité pour les sommets Pairs => /2 (car on a 2 choix)
=> loi de parité pour les centres => /2 (car on a 2 choix)
Finalement le nombre d'états du Skewb vaut:
g = 4!.34 x 4!.34 x 6! /3.3. 2.2.2


Donc avant de parler le nombre d'états d'un Cube, il faut fixer le Cube (orienter le Cube), traditionnellement on fixe le Cube ainsi :
Haut=blanc, Bas=jaune, Avant=vert, Postérieur=klein, Gauche=orange, Droite=rouge
ET préciser quels sont les rotations standards (les rotations de base)
Les configurations provenant des rotations standards se nomment les états du Cube.
Par ex
=> pour l'Helicopter les rotations standards sont les 12 rotations d'arêtes à 180°, les autres rotations sont non-standards
=> pour le Rubik's Cube les rotations standards sont {H,B,A,P,G,D} , les autres rotations tranches h,d,a ... sont non-standards
Quand on parle d'états du Rubik's Cube ce sont des états provenant des rotations de base {H,B,A,P,G,D}.
=> Pour le Skewb , les rotations standards sont les 8 rotations sommets à 120°.
Exemples :
==========
Le nombre d'états du Rubik's Cube
=============================
Pour calculer le nombre d'états du Rubik's Cube on suit la recette suivante:
Pour le Rubik's Cube:
=> On a 12 arêtes qui baladent partout en restant dans leur camp, donc le nombre de permutations est 12! (à connaitre par coeur)
=> Chaqu' arête a 2 orientations, donc le nombre d'orientations est 212 (à connaitre par coeur)
=> On a 8 sommets qui baladent partout en restant dans leur camp, donc le nombre de permutations est 8!
=> Chaque sommet a 3 orientations, donc le nombre d'orientations est 38
donc le nombre de configurations est :
12!.212 x 8!.38
Mais on a des contraintes (des lois), pour avoir le nombre d'états il faut donc diviser le nombre de configurations par les contraintes:
=> loi des flips => /2 (car on a 2 choix)
=> loi des twists => /3 (car on a 3 choix)
=> loi de parité => /2 (car on a 2 choix)
Finalement le nombre d'états du Rubik's Cube vaut:
g = 12!.212 x 8!.38 /2.3.2
==========
Le nombre d'états du Revenge
=============================
Pour calculer le nombre d'états du Revenge on suit la recette suivante:
Pour le Revenge:
=> On a 8 sommets qui baladent partout en restant dans leur camp, donc le nombre de permutations est 8!
=> Chaque sommet a 3 orientations, donc le nombre d'orientations est 38
=> On a 24 ailes qui baladent partout en restant dans leur camp, donc le nombre de permutations est 24! (à connaitre par coeur)
=> On a 24 centres qui baladent partout en restant dans leur camp, donc le nombre de permutations est 24!
donc le nombre de configurations est :
8!.38 x 24! x 24!
Mais on a des contraintes (des lois), pour avoir le nombre d'états il faut donc diviser le nombre de configurations par les contraintes:
=> loi des twists => /3 (car on a 3 choix)
=> loi de parité (sommets et centres en phase) => /2 (car on a 2 choix)
=> visuellement identique => /(4!6/2) (le nombre permutations des centres)
Finalement le nombre d'états du Revenge vaut:
g = 8!.38 x 24! x 24! /3 .2 . (4!6/2)
g = 8!.37 x (24!)² / 4!6
Le nombre d'états du Skewb
=========================
Les sommets du Skewb sont divisés en deux camps : le camp Impair et le camp Pair

Pour le Skewb:
=> On a 4 sommets Impairs qui baladent partout dans son camp, donc le nombre de permutations est 4! (à connaitre par coeur)
=> Chaque sommet Impair a 3 orientations, donc le nombre d'orientations est 34 (à connaitre par coeur)
=> On a 4 sommets Pairs qui baladent partout dans son camp, donc le nombre de permutations est 4! (à connaitre par coeur)
=> Chaque sommet Pair a 3 orientations, donc le nombre d'orientations est 34 (à connaitre par coeur)
=> On a 6 centres qui baladent partout en restant dans leur camp, donc le nombre de permutations est 6!
donc le nombre de configurations est :
4!.34 x 4!.34 x 6!
Mais on a des contraintes (des lois), pour avoir le nombre d'états il faut donc diviser le nombre de configurations par les contraintes:
=> loi des twists pour les sommets Impairs => /3 (car on a 3 choix)
=> loi des twists pour les sommets Pairs => /3 (car on a 3 choix)
=> loi de parité pour les sommets Impairs => /2 (car on a 2 choix)
=> loi de parité pour les sommets Pairs => /2 (car on a 2 choix)
=> loi de parité pour les centres => /2 (car on a 2 choix)
Finalement le nombre d'états du Skewb vaut:
g = 4!.34 x 4!.34 x 6! /3.3. 2.2.2