Les 3 antagonismes du Rubik's Cube
Publié : Ven 23/04/2021 11:55
Il y a 3 antagonismes du Rubik's Cube : Formule , Etat, Permutation (des autocollants), et il y a beaucoup de confusions ......
Les formules
==> Imaginez qu'on a un Rubik's Cube monochrome ! comme ceci

On a donc 6 rotations de base : {H,B,A,P,G,D}
Une formule V est une suite finie de rotations de base (et leur inverse sous entendu).
par ex : V = D' B D B' H' D B H' D B' D' H²
Donc une rotation de base est une formule..
M = <H,B,A,P,G,D>
M = l'ensemble des formules.
Les états
==> Un autre antagonisme, quand on applique une formule sur l'état résolu du Cube, les pièces bougent et changent l'orientation ce qui donne un état s=(u,x,v,y)
u=permutation des arêtes
x=orientation des arêtes
v=permutation des sommets
y = orientation des sommets
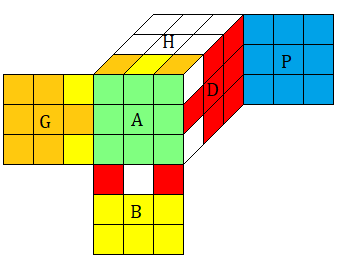
état s=(u,x,v,y) ; une sorte de motif
u=(1,9) , x=0
v=(1,5,6,2) , y = (-1,1,0,0,1,-1,0,0)
Pour retrouver ces donnés il faut connaitre le diagramme d'orientation et numérotation ci-dessous
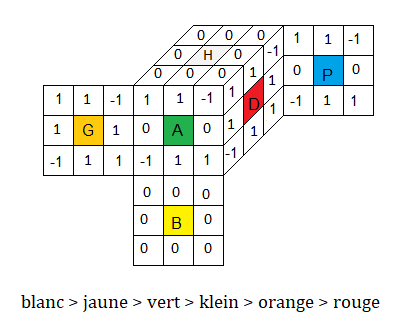
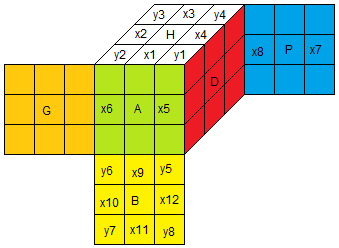
on regarde :
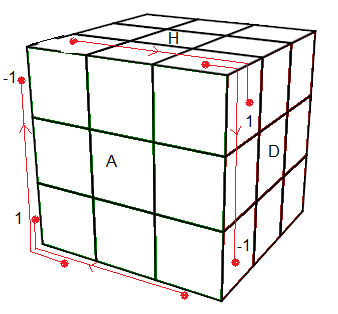
et on trouve
y1=-1, y2=1, y3=0, y4=0, y5=1, y6=-1, y7=0, y8=0
G = l'ensemble des états
Les permutations
==> Un dernier antagonisme , les permutations :
soit X = {1,2,3,...,48} l'ensemble des 48 autocollants éparpillés sur la table et numérotées ainsi.
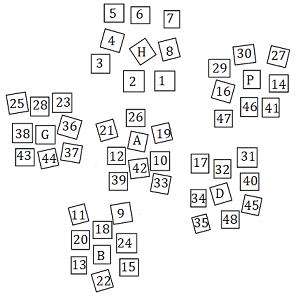
à chaque rotation de base {H,B,A,P,G,D} on associe une permutation :
pH = (2,4,6,8)(26,28,30,32) (1,3,5,7)(17,21,25,29)(19,23,27,31) ;
pB := (18,24,22,20)(42,48,46,44) (9,15,13,11)(33,45,41,37)(35,47,43,39);
pA := (2,34,18,36)(26,10,42,12) (1,35,11,23)(9,37,3,17)(19,33,39,21);
pP := (6,38,22,40)(30,14,46,16) (7,25,13,45)(29,27,41,47)(31,5,43 ,15);
pG := (4,12,20,14)(28,36,44,38) (3,39,13,27)(21,11,41,5)(23,37,43,25);
pD := (8,16,24,10)(32,40,48,34) (1,29,15,33)(17,31,45,35)(19,7,47,9);
On a donc 6 permutations de S48.
Soit Λ l'ensemble des permutations engendrées par les 6 permutations {PH, PB, PA, PP,PG, PD}
Λ = < PH, PB, PA, PP,PG, PD >
Trois antagonismes M, G, Λ
Ces trois ensembles sont en bijection, ça signifie qu'ils ont le même nombre d'éléments. |M| = |G| = |Λ|
On voit donc il y a de grande différence entre V, s, PV
¤ V = formule
¤ s = état
¤ pV = permutation (des autocollants)
formule ≠ état ≠ permutation des autocollants
Les formules
==> Imaginez qu'on a un Rubik's Cube monochrome ! comme ceci

On a donc 6 rotations de base : {H,B,A,P,G,D}
Une formule V est une suite finie de rotations de base (et leur inverse sous entendu).
par ex : V = D' B D B' H' D B H' D B' D' H²
Donc une rotation de base est une formule..
M = <H,B,A,P,G,D>
M = l'ensemble des formules.
Les états
==> Un autre antagonisme, quand on applique une formule sur l'état résolu du Cube, les pièces bougent et changent l'orientation ce qui donne un état s=(u,x,v,y)
u=permutation des arêtes
x=orientation des arêtes
v=permutation des sommets
y = orientation des sommets

état s=(u,x,v,y) ; une sorte de motif
u=(1,9) , x=0
v=(1,5,6,2) , y = (-1,1,0,0,1,-1,0,0)
Pour retrouver ces donnés il faut connaitre le diagramme d'orientation et numérotation ci-dessous


on regarde :

et on trouve
y1=-1, y2=1, y3=0, y4=0, y5=1, y6=-1, y7=0, y8=0
G = l'ensemble des états
Les permutations
==> Un dernier antagonisme , les permutations :
soit X = {1,2,3,...,48} l'ensemble des 48 autocollants éparpillés sur la table et numérotées ainsi.
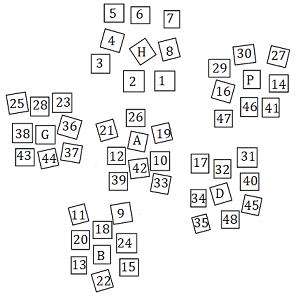
à chaque rotation de base {H,B,A,P,G,D} on associe une permutation :
pH = (2,4,6,8)(26,28,30,32) (1,3,5,7)(17,21,25,29)(19,23,27,31) ;
pB := (18,24,22,20)(42,48,46,44) (9,15,13,11)(33,45,41,37)(35,47,43,39);
pA := (2,34,18,36)(26,10,42,12) (1,35,11,23)(9,37,3,17)(19,33,39,21);
pP := (6,38,22,40)(30,14,46,16) (7,25,13,45)(29,27,41,47)(31,5,43 ,15);
pG := (4,12,20,14)(28,36,44,38) (3,39,13,27)(21,11,41,5)(23,37,43,25);
pD := (8,16,24,10)(32,40,48,34) (1,29,15,33)(17,31,45,35)(19,7,47,9);
On a donc 6 permutations de S48.
Soit Λ l'ensemble des permutations engendrées par les 6 permutations {PH, PB, PA, PP,PG, PD}
Λ = < PH, PB, PA, PP,PG, PD >
Trois antagonismes M, G, Λ
Ces trois ensembles sont en bijection, ça signifie qu'ils ont le même nombre d'éléments. |M| = |G| = |Λ|
On voit donc il y a de grande différence entre V, s, PV
¤ V = formule
¤ s = état
¤ pV = permutation (des autocollants)
formule ≠ état ≠ permutation des autocollants
ATTETION !! ne pas confondre entre pH et u , v
pH ==> permutation des autocollants
u , v ==> permutations des pièces : u ==> arêtes, v ==> sommets