Les motifs

[Morphocode]

Il était une fois un riche marchant de tapis ... Il possèdait deux tapis avec deux motifs M1 et M2 ci-dessous,



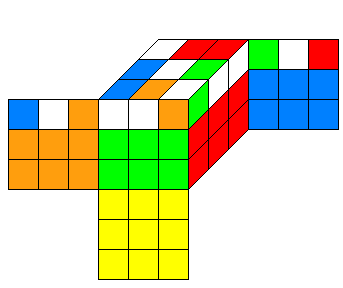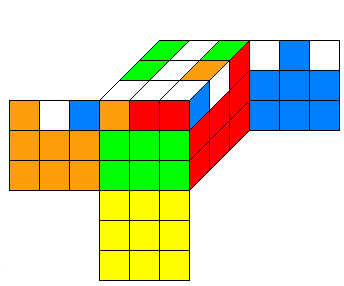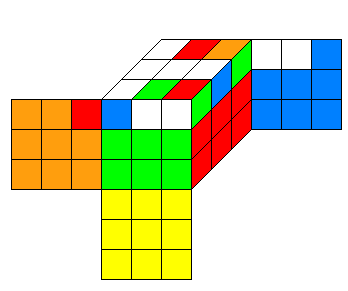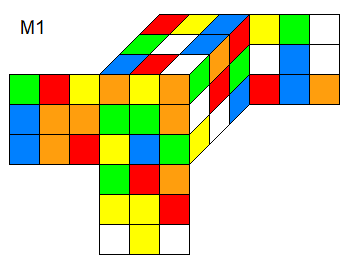
ces deux tapis plutôt ces deux motifs sont très précieux pour lui , il ne les sépare jamais.
Un jour il devait quitter le pays pour vivre dans un autre pays, mais les lois de son pays ne lui autorise d'amener qu'un seul tapis (un seul motif) et il est interdit de reproduire ces deux motifs de quelle façon que ce soit, sous peine de mort !
Alors le marchant se demandait s'il était possible de "combiner" ces deux motifs M1 et M2 pour avoir un troisième M3, ainsi comme le motif M3 n'est pas interdit il pourrait alors amener le motif M1 et M3 ou M2 et M3 et quand il serait dans l'autre pays il pourrait "recombiner" le motif M1 et M3 pour avoir M2 ou M2 et M3 pour avoir M1 ?
Il donne une récompense de 30 millions de dollars pour celui qui arrive à combiner ces deux motifs M1 et M2 comme il désirait.
alors ?? .....qui veut devenir riche ???

[Morphocode]

Ce que demande le marchant est difficile à réaliser , en effet il faut :
1) associer un état (nous dirons "état" plutôt que "motif") à un objet mathématique (pour faire des calculs)
2) on peut effectuer des opérations sur ces objets (combiner ces objets)
3) l'opération doit avoir des propriétés (on veut extraire un état)

Heureusement , toutes ces condictions sont réalisées ! on a vraiment de la chance !!
Pour simplifier les écritures (on est paresseux d'écrire des trucs trop long !) on suppose que seulement le Haut est mélangé, le reste du Cube est intact.

un état s, est codé par: s = (u,x,v,y) où
u=permutation-arêtes, x=orientation-arêtes
v=permutation-sommets, y=orientation-sommets

et l'opération (le produit) de s et s'=(u',x',v',y') est par définition vaut :
ss' = (uu', x+u(x'), vv',y+v(y')).
et on trouve facilement s-1 (état inverse de s) , en effet il suffit de prendre s'= s-1 et on a:
ss' = id = (uu', x+u(x'), vv',y+v(y')) = (id,0,id,0)
uu' = id ===> u' = u-1
x+u(x') = 0 ===> x' = u-1(-x)
de même pour v et y
donc s-1 vaut :
s-1= (u-1,u-1(-x), v-1,v-1(-y))


exemple on prend deux états m1 et m2 suivants:

m1 = (u,x,v,y) avec u=(1,4,3,2), x=(1,1,1,1) , v=(1,4,3,2), y=(-1,0,1,0)


m2 = (u',x',v',y') avec u'=(1,2,4), x'=(1,1,0,0) , v'=(1,4)(2,3), y'=(1,-1,0,0)


Le calcul montre m1.m2 = m3 vaut

m3 = (p,z,q,t) avec p=(3,4), z=(1,0,0,1) , q=(2,4), t=(-1,1,0,0)

on a:
(m1)-1 = (u,x,v,y) avec u=(2,3,4,1), x=(1,1,1,1) , v=(2,3,4,1), y=(0,-1,0,1)

Le marchant peut donc emporter les motifs m1 et m3 , une fois arrivé dans son nouveau pays , il peut recombiner le motif m1 et m3 pour retrouver m2.
(m1)-1m3 = m2