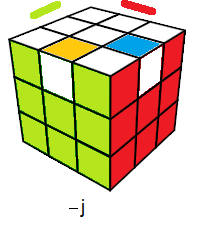Fan2Cube

INTRODUCTION
=============

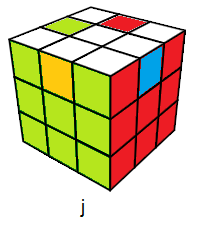
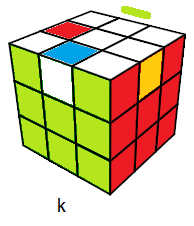
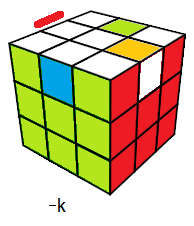
Certains états du Rubik's Cube repérentent des nombres ! et ce sont des nombres très célèbres !!
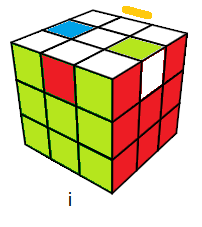
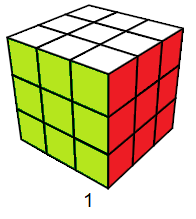
Intutifvement on peut dire que l'état résolu représente le nombre 1, comme ça sans justification ... bref est-il vrai ? cette intuition ? ....
Nous allons voir .
Pour simplifier on supose que le Rubik's Cube est mélangé seulement les 4 arêtes-Haut le reste du Cube reste intact. Si on veut savoir combien y-a-t-il ce genre de configurations ? le calcul donne:
4 arêtes à déplacer ==> 4! = 24 permutations
chaqu'arête a 2 orientations et on a 4 arêtes ==> 24 = 16 orientations
total : 4! x 24 = 24 x 16 = 384 états
C'est le nombre maximum qu'on peut avoir, en réalité le nombre d'états est plus petit car on a des contrains dans le déplacement et dans l'orientation des arêtes. par exemple on ne peut pas orienter une seule arête ! ni déplacer seulement 2 arêtes !!!
plus précisement :
4! x 24 /(2 x 2) = 96 états arêtes-Haut (/2 ==> permutations pair, /2 ==> pivoter toujours 2 arêtes)

Parmi ces 96 états il y a des états qui représentent des nombres !!
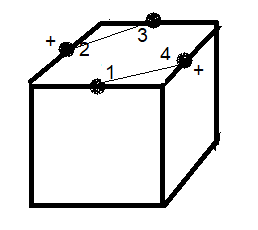
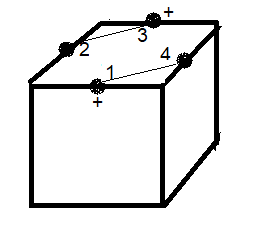
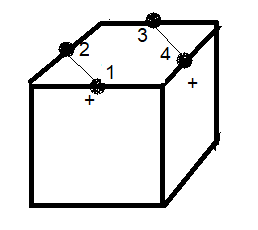
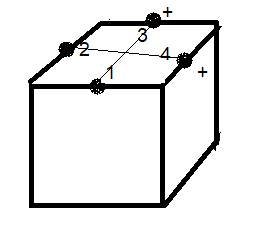
On va numéroter les arêtes comme montre le dessein ci-dessous


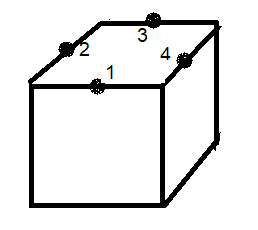
Un état s est décrit par (u,x ) où u=permutation, x=(x1,x2,x3,x4) vecteur d'orientation.
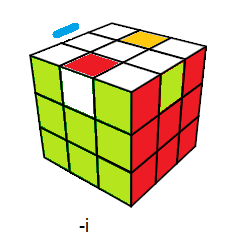
exemple
s = (u,x)
u = 1->4->3
x=(0,1,1,0) , x1=0,x2=1,x3=1,x4=0
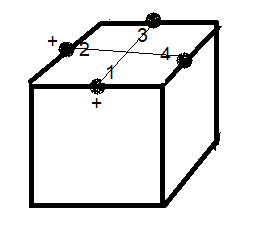
sur le dessin on cherche où se trouve x2 et on marquera un "+" de même
sur le dessin on cherche où se trouve x3 et on marquera un "+"
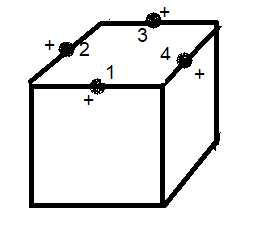
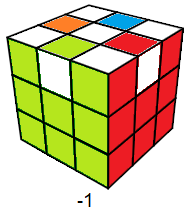
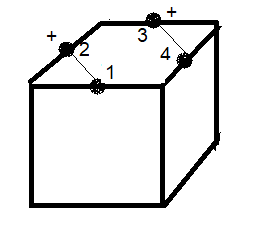
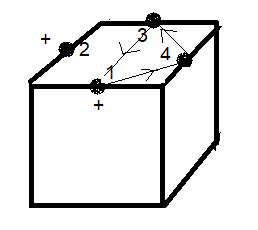
voici le dessin correspond à l'état s.

On démontre mathématiquement que l'état a ci-dessous représente le nombre complexe i !!!!
a=(u,x)
u=(1,4)(2,3)
x=(1,0,1,0), x1=1,x2=0,x3=1,x4=0


C'est vraiment merveilleux que le Rubik's Cube contient i , en effet le nombre complexe i est un objet mathématique étrange car il a la propriété i²=-1 alors que le carré d'un nombre réel est toujours positif comme 3²=9 ou (-4)² =16.
On se demande si le Rubik's Cube contient d'autres nombres ? voyons:

¤ on a i²=-1 puisque l'état a correspond à i, calculons donc a²
rappelle le produit de 2 états s et s'
s=(u,x) , s'=(u',x')
ss' = (uu', x+u(x')) ; u(x')=on permute les x'1, x'2, x'3, x'4 par u
calculons a² avec
a=(u,x)
u=(1,4)(2,3)
x=(1,0,1,0)
a² = (uu,x+u(x))
u²=id
x+u(x)=(1,0,1,0)+u(x1,x2,x3,x4)=(1,0,1,0)+(x4,x3,x2,x1)=(1,0,1,0)+(0,1,0,1)=(1,1,1,1)=t
a²=(id,t) avec t=(1,1,1,1)
et le dessein correspond


cet état correspond au nombre -1, c'est le MiniFlip = 4 arêtes Haut flippées

¤ on a i4 = 1, calculons donc l'état a4
a²=(id,t) où t=(1,1,1,1)
a4 =(id,t)(id,t)
id²=id
(1,1,1,1)+id(1,1,1,1)=(1,1,1,1)+(1,1,1,1)=(2,2,2,2)=(0,0,0,0)=0 (mod 2) ; si on pivote 2 fois on pivote rien du tout .
a4 = (id,0) c'est l'état résolu !!! personne ne bouge et toutes les pièces sont bien orientées
donc l'état résolu e représente le nombre "1" , notre intution est justifié.


¤ on a i² = -1 ==> i3 = -i , calculons donc l'état a3
a²=(id,t) où t=(1,1,1,1)
a=(u,x) où x=(1,0,1,0)
a3=a²a=(id,t)(u,x)=(p,z)
p = id u = u
z=(1,1,1,1)+id(1,0,1,0)=(1,1,1,1)+(1,0,1,0)=(2,1,2,1)=(0,1,0,1) (mod 2)
a3 = (u,z) où z=(0,1,0,1) cet état représente -i.



RESUMONS :
===============
Nous avons 4 états qui représent 4 nombres :

a = i
a² = -1
a4 = 1
a3 = -i





Et les formules correspondantes
i ⇒ D P' A D' P A' H P H P' A D' A' D' (minimale,14)
-1 ⇒ A' H' G' H P' H² P G H A H' D H² D' (minimale,16)
-i ⇒ D A D P A' H' P' H' P' A D P A' D' (minimale,14)
1 ⇒ I

C'est surprenant hein ????

Il y a un autre nombre baptisé quaternion j, il est différent du nombre complexe i mais possède les même propriétés du genre j²=-1 ....
On démontre alors que l'état suivant représente j:
b = (m,x)
m = (1,2)(3,4)
x = (1,0,0,1)
b ----> j



Le même calcul nous donne:
b² = (id,t) ----> -1
b3 = b²b = (id,t)( (m ,x) = (m,w)
w = (1,1,1,1)+id(1,0,0,1) = (1,1,1,1)+(1,0,0,1) = (0,1,1,0) (mod 2)
b3 = (m,w) où w=(0,1,1,0)
b3 ----> -j



Et rien ne nous empêche de calculer ab !!!
calculons donc ab = c = (µ,x)
µ = (1,4)(2,3)(1,2)(3,4) = (1,3)(2,4)
x = (1,0,1,0)+u(1,0,0,1) = (1,0,1,0)+(1,0,0,1) = (0,0,1,1)
donc c vaut
c = ( µ,x) où x=(0,0,1,1)
ab ----> ij
c ---->k



de même pour -k
c3 ----> -k



En résumé , le Rubik's Cube contient 8 nombres :
H = {1, i, j, k, -1, -i, -j, -k}
Les plus connus:
Les entiers: 1,-1,
Les complexes: i, -i ,
Les moins connus :
Les quaternions : j,k,-j,-k

1 (entier), i (complexe), j (quaternion), k (quaternion)