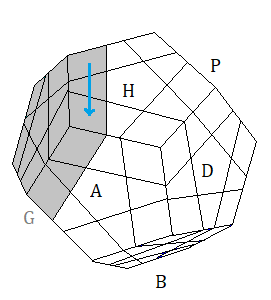
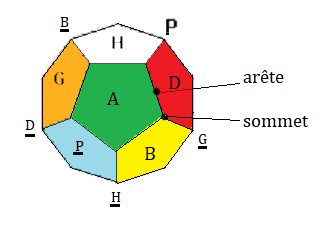
Pyraminx :

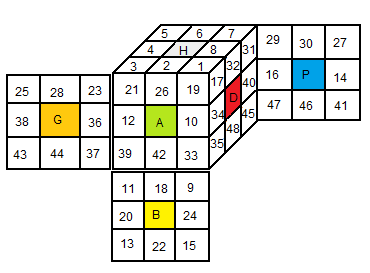
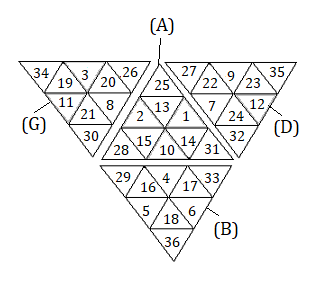
Les autocollants (stickers) sont numérotés comme indique la fig ci-dessous
Numérotation des autocollants :
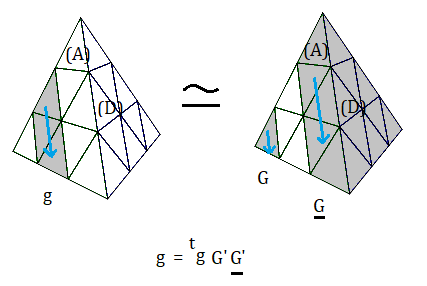
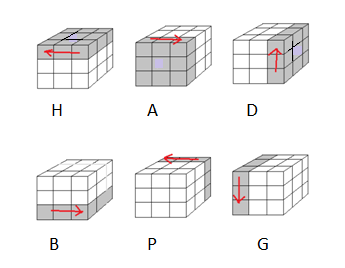
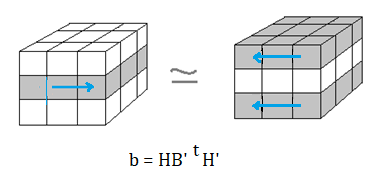
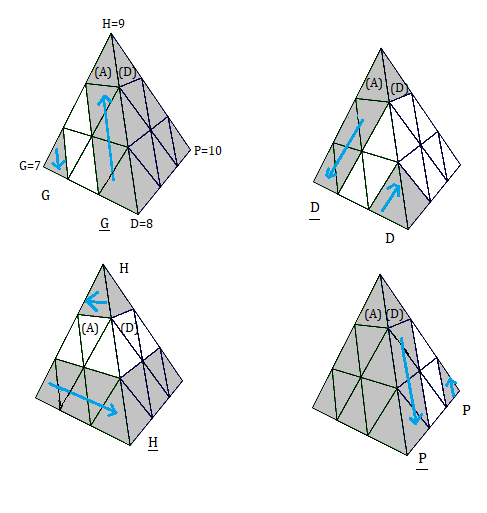
On définit les 8 rotations {G, D, H, P, G, D, H, P} (G = rotation-opposée à G) comme ceci :
On pose :
Q = < GG', DD' , HH', PP' >
Q engendre un ensemble d'états S défini ainsi :
S = { s = état | s = e•V , V∈Q } ; e=état résolu
Par définition S est le groupe Glissant (Slice group) du Pyraminx .
Le GAP nous donne
|S| = 302330880
Voici un script en GAP qui permet de trouver |S|
Code : Tout sélectionner
#gap_pyraminx.txt
#permutations de base
#permutation sommet
pG := (30,28,29);
pD := (33,31,32);
pH := (27,25,26);
pP := (35,34,36);
#per tranche: (arete)(arete)(centre)
pg := (2,4,11)(8,10,5)(21,15,16);
pd := (1,12,4)(7,6,10)(17,14,24);
ph := (1,8,9)(7,2,3)(22,13,20);
pp := (3,5,12)(9,11,6)(23,19,18);
#per-croisée
pGs := (1,3,6)(7,9,12)(13,19,17)(14,20,18)(22,23,24)(25,34,33)(26,36,31)(27,35,32);
pDs := (2,5,9)(3,8,11)(13,16,23)(15,18,22)(19,20,21)(25,29,35)(26,30,34)(27,28,36);
pHs := (4,6,5)(10,12,11)(14,23,21)(15,24,19)(16,17,18)(28,32,34)(29,33,36)(30,31,35);
pPs := (1,2,10)(4,7,8)(13,15,14)(16,24,20)(17,22,21)(25,28,31)(26,29,32)(27,30,33);
#permutations étendues (violer les lois)
pGamma := (1,7);
pOmega := (1,2)(7,8);
####
LAMBDAPLUS := Group( pG, pD, pH, pP, pg, pd, ph, pp, pGamma, pOmega );
LAMBDA := Group( pG, pD, pH, pP, pg, pd, ph, pp);
GLISSANT := Group(pG*pGs^-1, pD*pDs^-1, pH*pHs^-1, pP*pPs^-1);
N := 2*2 ;;
Print( "\n" );
Print( "|LAMBDA+| = ",Size( LAMBDAPLUS ), "\n" );
Print( "|LAMBDA| = ", Size( LAMBDA ) , "\n" );
Print( "|GLISSANT| = ", Size( GLISSANT ) , "\n" );
Print( "N = ",N , "\n" );
Print( "|G+| = ", Factorial(6) * (2^6) * (3^4) *(3^4), "\n" );
Print( "|G| = |G+|/N = ", (Factorial(6) * (2^6)*(3^4)*(3^4)) / N, "\n" );
On trouve :
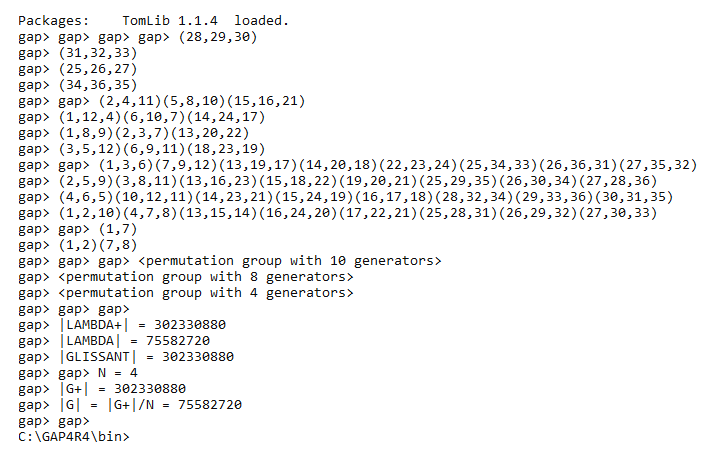
Remarque : On a: