Les groupes Croisés (Cross group) des twists platoniques
Publié : Ven 8/03/2024 19:22
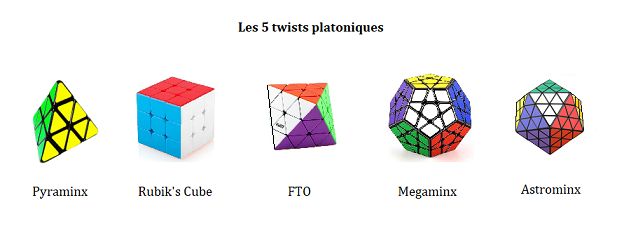
Les 5 twists de Platon :
Le groupe Croisé du Pyraminx
Pyraminx :

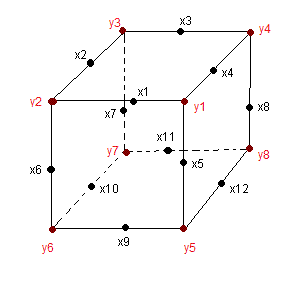
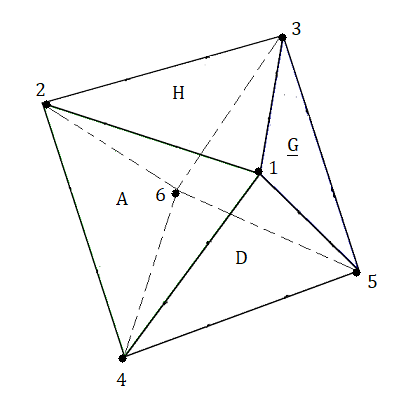
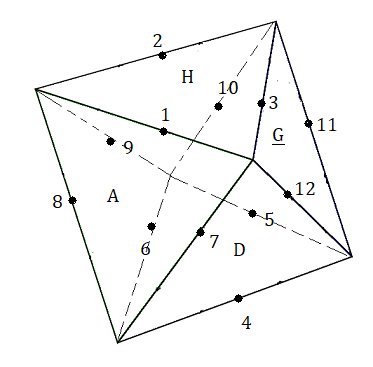
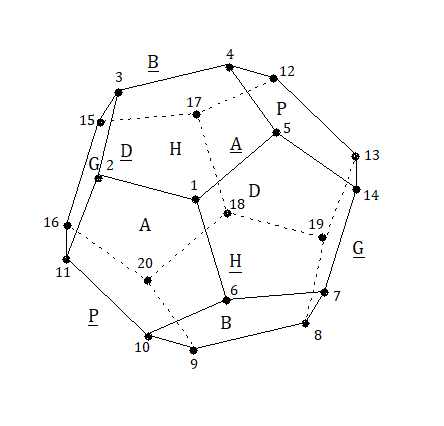
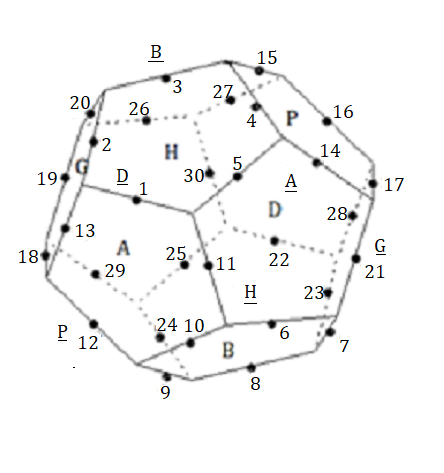
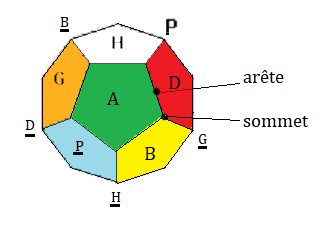
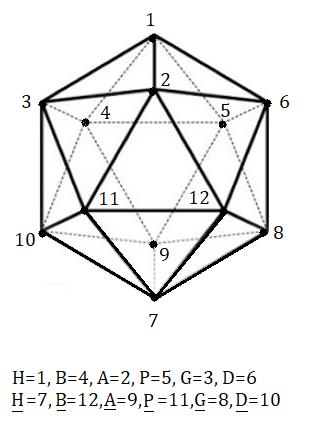
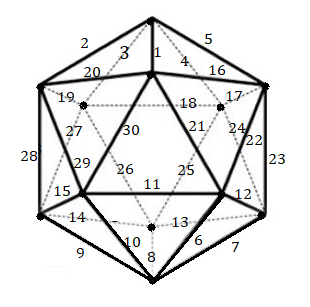
On ignore les orientations, les sommets et les arêtes sont identifiés par un numéro comme indique la fig ci-dessous
Numérotation des pièces :
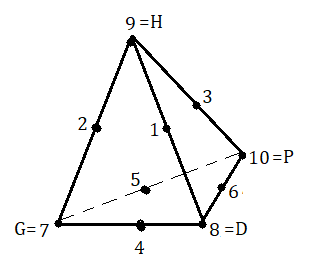
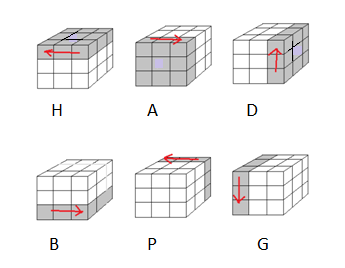
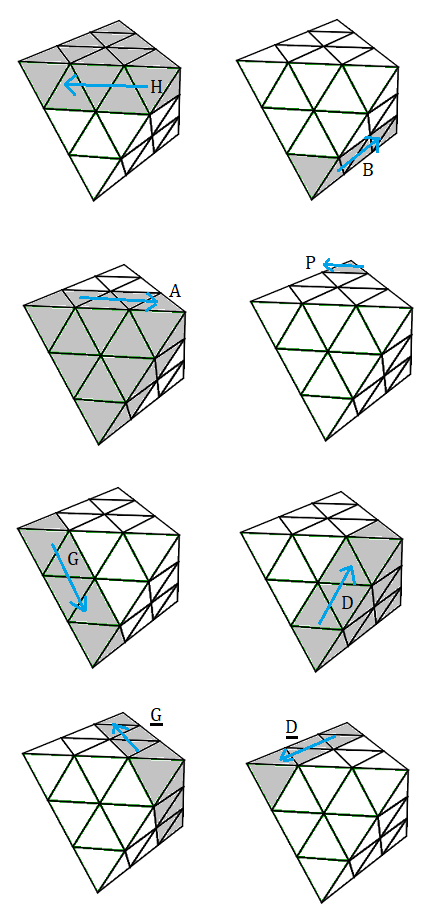
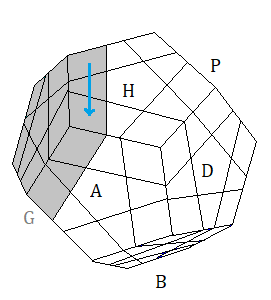
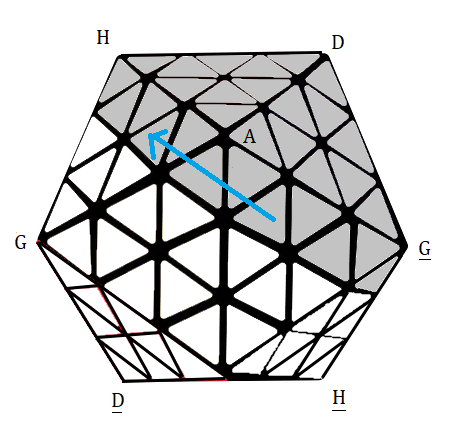
On définit les 4 rotations (rotations-croisées) comme ceci :
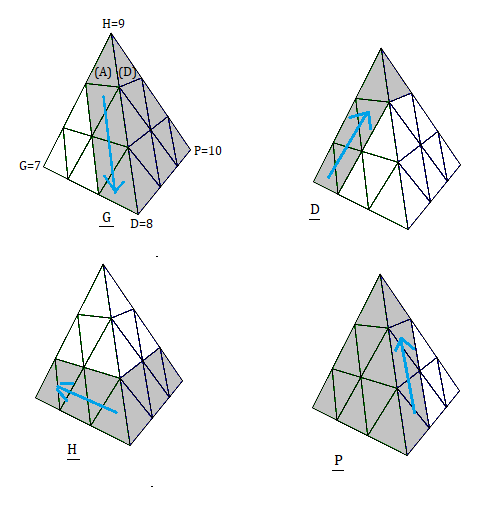
Une rotation-croissé c'est une rotation qui déplace les sommets et les arêtes .
On pose : (formules croisées)
K = < XY' | X,Y ∈{ G ,D , H , P } >
* K engendre un groupe de permutations des sommets Cs = C, par définition C est le groupe Croisé du Pyraminx .
* K engendre aussi un groupe de permutations des arêtes Ca, par définition Ca est le groupe Croisé des arêtes .
Voici un script en GAP qui permet de trouver C et Ca
On trouve :
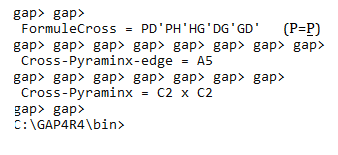
Commentaire : C2 x C2 = Z2 x Z2 = K = le groupe Klein , c'est le seul groupe à 4 éléments non-cyclique , assez célèbre
A5 = Premier groupe simple non abélien ==> donc célèbre aussi

Le groupe Croisé du Pyraminx
Pyraminx :

On ignore les orientations, les sommets et les arêtes sont identifiés par un numéro comme indique la fig ci-dessous
Numérotation des pièces :

On définit les 4 rotations (rotations-croisées) comme ceci :

Une rotation-croissé c'est une rotation qui déplace les sommets et les arêtes .
On pose : (formules croisées)
K = < XY' | X,Y ∈{ G ,D , H , P } >
* K engendre un groupe de permutations des sommets Cs = C, par définition C est le groupe Croisé du Pyraminx .
* K engendre aussi un groupe de permutations des arêtes Ca, par définition Ca est le groupe Croisé des arêtes .
Voici un script en GAP qui permet de trouver C et Ca
Code : Tout sélectionner
#FormuleCroise = < XY' | X,Y rotations-croisée >
#Le groupe croisé du Pyraminx (tétraèdre :S=4,F=4,A=6)
Twist := "Pyraminx";
#les rotations-croisées des sommets (Cross vertice)
vG := (10,8,9);
vD := (7,10,9) ;
vH := (10,7,8) ;
vP := (8,7,9) ;
SX := [vG, vD, vH, vP];;
SYp := [vG^-1, vD^-1, vH^-1, vP^-1];;
SXtxt := ['G', 'D', 'H', 'P'];; #rotation-croisée, G=Gsouligné
SYptxt := ['g', 'd', 'h', 'p'];; #g=inverse de G
rot:=4;
#les rotations-croisées des arêtes (Cross edge)
uG := (3,6,1) ;
uD := (5,3,2) ;
uH := (6,5,4) ;
uP := (4,2,1) ;
AX := [uG, uD, uH, uP];;
AYp := [uG^-1, uD^-1, uH^-1, uP^-1];;
# fonction donne au hasard une formule-croisée de longueur 2n
RandomCrossFormula := function(n)
local nombre, permutations, k , formule, m ;
nombre := List([1..n], i -> RandomList([1..rot]));; #[1..4] ==> 4 rotations
#Print("\n listnombre = ", nombre , "\n" );
permutations := [];
formule := [];
for k in nombre do
Append(permutations,[SX[k]]); # pour le calcul
Append(formule,[SXtxt[k]]); # pour affichage
m := RandomList([1..rot]);
while k=m do
m := RandomList([1..rot]);
od;
Append(permutations, [SYp[m]]);
Append(formule,[SYptxt[m]]);
od;
Product(permutations); # calculer le resultat
# affichage
formule := ReplacedString( formule, "g", "G'" );;
formule := ReplacedString( formule, "d", "D'" );;
formule := ReplacedString( formule, "h", "H'" );;
formule := ReplacedString( formule, "p", "P'" );;
return formule;
end;
Print("\n FormuleCross = ", RandomCrossFormula(5) , "\n" );
############
generators := Set(Arrangements([1..rot],2), t -> AX[t[2]] * AYp[t[1]]);; #[1..4] ==> 4 rotations
#Print("\n generateur = ", Length(generators) , "\n" );
Cross := Group(generators);;
Cedge := Size(Cross) ;;
#IsSimpleGroup( Cross ) ;
Print("\n ",Twist,"-Cross-edge = ", StructureDescription(Cross) ," (",Cedge, ") \n" );
generators := Set(Arrangements([1..rot],2), t -> SX[t[2]] * SYp[t[1]]);; #[1..4] ==> 4 rotations
#Print("\n generateur = ", Length(generators) , "\n" );
Cross := Group(generators);;
Cvertex := Size(Cross) ;;
#IsSimpleGroup( Cross ) ;
Print("\n ",Twist,"-Cross = ", StructureDescription(Cross) ," (",Cvertex, ") \n" );
On trouve :
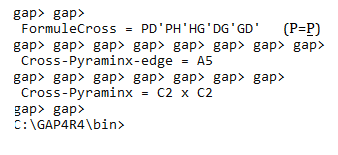
Commentaire : C2 x C2 = Z2 x Z2 = K = le groupe Klein , c'est le seul groupe à 4 éléments non-cyclique , assez célèbre
A5 = Premier groupe simple non abélien ==> donc célèbre aussi