1) Déplacer 3 arêtes
2) Inverser deux arêtes
3) SuperFlip (toutes les arêtes sont renversées)
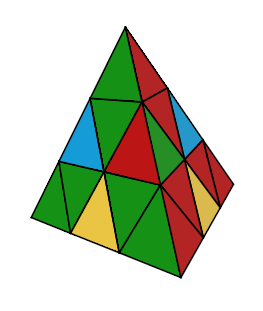
Numérotation des autocollants
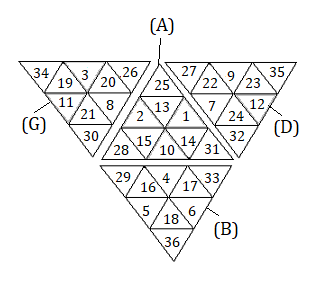
Les rotations tranches
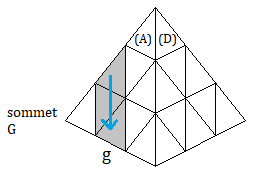
On veut trouver une formule qui déplace ces arêtes
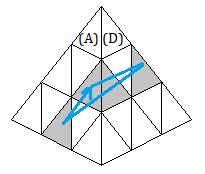
On veut trouver une formule qui inverse ces arêtes
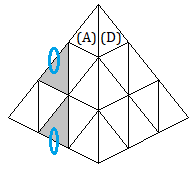
On veut trouver une formule pour le SuperFlip (toutes les arêtes sont renversées)
Voici un petit script en GAP qui répond à la question.
On se donne la permutation, et on doit trouver la formule
Code : Tout sélectionner
#gap_pyraminx.txt
#permutations sommets
pG := (30,28,29);;
pD := (33,31,32);;
pH := (27,25,26);;
pP := (35,34,36);;
#permutations tranches: (arete)(arete)(centre)
pg := (2,4,11)(8,10,5)(21,15,16);;
pd := (1,12,4)(7,6,10)(17,14,24);;
ph := (1,8,9)(7,2,3)(22,13,20);;
pp := (3,5,12)(9,11,6)(23,19,18);;
#permutations étendues (violer les lois)
pGamma := (1,7);;
pOmega := (1,2)(7,8);;
#LAMBDAPLUS := Group( pG, pD, pH, pP, pg, pd, ph, pp, pGamma, pOmega );;
LAMBDA := Group( pG, pD, pH, pP, pg, pd, ph, pp);;
#Print("\n [dh] = ",pd*ph*pd^-1*ph^-1, "\n" );
#Print("\n [dh'][g'h] = ",pd*ph^-1*pd^-1*ph* pg^-1*ph*pg*ph^-1, "\n" );
#Print("\n [gd'] = ",pg*pd^-1*pg^-1*pd, "\n" );
#Les rotations de base
rotbase := EpimorphismFromFreeGroup(LAMBDA:names:=["G", "D", "H", "P", "g", "d", "h", "p"]);;
# ou bien
#M := FreeGroup("G","D","H","P","g","d","h","p");;
#rotbase := GroupHomomorphismByImages( M, LAMBDA, GeneratorsOfGroup(M),GeneratorsOfGroup(LAMBDA) );;
per1 := (2,8)(4,10) ;;
pertxt1 := "(AG)+(BA)+" ;; # [dh] ; hg'pg'p'g h'g (8)
#per2 := (1,9,4)(3,10,7);;
#pertxt2 := "(BA,AD,GD)" ;;# [dh'][g'h] ; gdhgh'g'd'gd'gdp'h'pdhd' (17)
#per3 := (1,2,4)(7,8,10);;
#pertxt3 := "(AD,AG,BA)" ;;# [gd'] ; gd'g'd (4)
#per4 := (1,7)(2,8)(3,9)(4,10)(5,11)(6,12) ;;
#pertxt4 := "SuperFlip" ;;# hg'pg'p'gh'gdghg'h'd'g'pgdg'd'p'g'hg'h'd'g'dp'hph'g'dpd'pdp'2g'd' (42)
# on donne la permutation ==> trouver une formule (pas forcement la formule minimale)
per := per1 ;;
pertxt := pertxt1 ;;
formule := PreImagesRepresentative( rotbase, per );;
#affichage en clair
formule1 := String(formule);;
formule1 := ReplacedString( formule1, "^-1", "'" );;
formule1 := ReplacedString( formule1, "^-2", "'2" );;
formule1 := ReplacedString( formule1, "^2", "2" );;
formule1 := ReplacedString( formule1, "*", "" );;
Print("\n ",pertxt," = ", formule1," (",Length(formule),")", "\n" );
REMARQUE : GAP ne donne pas la formule minimale, mais une formule qui répond à la question.



