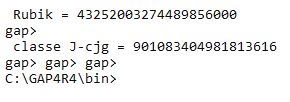
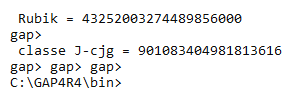
Le nombre de classes J-conjugaison du Rubik's Cube : 901083404981813616
Publié : Ven 2/02/2024 12:56
Le mystérieux nombre 901083404981813616
Ce nombre a fait coulé beaucoup d'encre ... parfois on dit que c'est le nombre d'états du Rubik's Cube !
En réalité ce sont des classes d'équivalence des états nommé les classes J-conjugaison .
Tout s'est passé vers les années 1994 ... On voulait chercher le diamètre du Rubik's Cube, mais le graphe des états
est trop gros, on voulait réduire ce graphe à un graphe de taille plus petit pour faciliter l'exploitation.
Jerry BRYAN a eu l'idée de classer les états suivant le critère nommé "J-conjugaison" où J est le groupe d'isométrie de cube (ce groupe a 48 éléments).
Le graphe de J-conjugaison est 48 fois plus petit donc l'exploration du graphe est plus vite.
Le symétrie J-conjugaison
---------------------------------
Les classes J-conjugaison définition1:
Définition1 : Les classes J-conjugaison (J=groupe isométrie du cube à 48 éléments)
Deux états s=e•V , V€M et t sont équivalents ssi :
il existe f∈J tel que e•(fVf-1) = t ; e=état résolu
Les classes de cette relation se nomment les classes J-conjugaison
Il y a une autre façon de définir les classes J-cojugaison .
On sait que J est inclus dans S48 grâce au théorème : K un goupe fini alors K est isomorphe à un sous groupe S|K|
Λ est aussi inclus dans S48
On va définir une relation d'équivalence sur Λ de la façon suivante:
Λ = < pH, pB, pA, pP, pG, pD >
Définition2 des classes J-cojugaison :
------------------------------------------
p,q ∈Λ sont équivalentes ssi : il existe f ∈J tel que fpf-1 = q
les classes de cette relation se nomment classes J-conjugaison
Le nombre de classes w est donné par la formule de Burnside :
w = 1/|J| Σ |Ff| ; sommer sur (f ∈J)
Ff = {p ∈ Λ | fpf-1 = p}
Ff = {p ∈ Λ | fp = pf}
On calcule w en GAP :
Ce nombre a fait coulé beaucoup d'encre ... parfois on dit que c'est le nombre d'états du Rubik's Cube !
En réalité ce sont des classes d'équivalence des états nommé les classes J-conjugaison .
Tout s'est passé vers les années 1994 ... On voulait chercher le diamètre du Rubik's Cube, mais le graphe des états
est trop gros, on voulait réduire ce graphe à un graphe de taille plus petit pour faciliter l'exploitation.
Jerry BRYAN a eu l'idée de classer les états suivant le critère nommé "J-conjugaison" où J est le groupe d'isométrie de cube (ce groupe a 48 éléments).
Le graphe de J-conjugaison est 48 fois plus petit donc l'exploration du graphe est plus vite.
Le symétrie J-conjugaison
---------------------------------
Les classes J-conjugaison définition1:
Définition1 : Les classes J-conjugaison (J=groupe isométrie du cube à 48 éléments)
Deux états s=e•V , V€M et t sont équivalents ssi :
il existe f∈J tel que e•(fVf-1) = t ; e=état résolu
Les classes de cette relation se nomment les classes J-conjugaison
Il y a une autre façon de définir les classes J-cojugaison .
On sait que J est inclus dans S48 grâce au théorème : K un goupe fini alors K est isomorphe à un sous groupe S|K|
Λ est aussi inclus dans S48
On va définir une relation d'équivalence sur Λ de la façon suivante:
Λ = < pH, pB, pA, pP, pG, pD >
Définition2 des classes J-cojugaison :
------------------------------------------
p,q ∈Λ sont équivalentes ssi : il existe f ∈J tel que fpf-1 = q
les classes de cette relation se nomment classes J-conjugaison
Le nombre de classes w est donné par la formule de Burnside :
w = 1/|J| Σ |Ff| ; sommer sur (f ∈J)
Ff = {p ∈ Λ | fpf-1 = p}
Ff = {p ∈ Λ | fp = pf}
On calcule w en GAP :
Code : Tout sélectionner
#gap_rubik-J-cjg-burnside.txt
#model Rubik's Cube en GAP
# 5 6 7
# 4 H 8
# 3 2 1
# 25 28 23 | 21 26 19 | 17 32 31 | 29 30 27
# 38 G 36 | 12 A 10 | 34 D 40 | 16 P 14
# 43 44 37 | 39 42 33 |35 48 45 | 47 46 41
# 11 18 9
# 20 B 24
# 13 22 15
# H=49,B=50,A=51,P=52,G=53,D=54
# Iso=le groupe isometries du cube (48 éléments)
j1 := (6,46,18,26)(8,14,24,12)(38,48,36,32)(2,30,22,42)(16,20,10,4)(28,40,44,34)
(5,45,11,17)(7,13,9,3)(21,31,41,35)(43,33,23,29)(1,25,15,37)(47,39,19,27) ;
j2 := (6,16,22,14)(8,24,20,4)(38,30,40,46)(2,10,18,12)(28,32,48,44)(34,42,36,26)
(5,31,15,43)(7,45,13,25)(21,19,33,39)(1,35,11,23)(47,41,27,29)(3,17,9,37);
Iso := Group(j1,j2) ;
#NrConjugacyClasses(Iso) ;
# Dep=le groupe isometrie+ (deplacement=rotation) du cube (24) Dep = ssg de Iso
#d1 := (1,11)(2,18)(3,9)(4,24)(5,15)(6,22)(7,13)(8,20)(10,12)
# (14,16)(17,37)(19,39)(21,33)(23,35)(25,45)(26,42)(27,47)(28,48)(29,41)
# (30,46)(31,43)(32,44)(34,36)(38,40);
#d2 := (1,15)(2,22)(3,13)(4,20)(5,11)(6,18)(7,9)(8,24)(10,16)(12,14)
# (17,45)(19,47)(21,41)(23,43)(25,37)(26,46)(27,39)(28,44)(29,33)(30,42)
# (31,35)(32,48)(34,40)(36,38) ;
#d3 := (1,17,19)(2,32,10)(3,31,33)(4,40,42)
# (5,45,39)(6,48,12)(7,35,21)(8,34,26)(9,23,29)(11,25,47)(13,43,41)
# (14,22,44)(15,37,27)(16,18,28)(20,38,46)(24,36,30);
#d4 := (1,35,11,23)(2,10,18,12)(3,17,9,37)(4,8,24,20)(5,31,15,43)
# (6,16,22,14)(7,45,13,25)(19,33,39,21)(26,34,42,36)(27,29,47,41)
# (28,32,48,44)(30,40,46,38) ;
#Dep := Group(d1,d2,d3,d4) ; #à 4 générateurs
#sgs := SmallGeneratingSet(Dep);
#Length(sgs);
d1 := (1,29,15,33)(2,6,22,18)(3,27,13,39)(4,38,20,36)(5,41,11,21)
(7,47,9,19)(8,40,24,34)(10,32,16,48)(12,28,14,44)(17,31,45,35)(23,25,43,37)(26,30,46,42);
d2 := (1,45,27)(2,48,14)(3,35,41)(4,34,46)(5,17,47)(6,32,16)(7,31,29)
(8,40,30)(9,43,21)(10,22,28)(11,37,39)(12,18,44)(13,23,33)(15,25,19)(20,36,42)(24,38,26);
Dep := Group (d1,d2) ; #à 2 générateurs
#NrConjugacyClasses(Dep) ;
#IsSubgroup(Iso, Dep) ;
# Rubik=le groupe des permutations du Rubik's Cube
pH := (2,4,6,8)(26,28,30,32) (1,3,5,7)(17,21,25,29)(19,23,27,31) ;
pB := (18,24,22,20)(42,48,46,44) (9,15,13,11)(33,45,41,37)(35,47,43,39);
pA := (2,34,18,36)(26,10,42,12) (1,35,11,23)(17,9,37,3)(19,33,39,21);
pP := (6,38,22,40)(30,14,46,16) (7,25,13,45)(29,27,41,47)(31,5,43 ,15);
pG := (4,12,20,14)(28,36,44,38) (3,39,13,27)(21,11,41,5)(23,37,43,25);
pD := (8,16,24,10)(32,40,48,34) (1,29,15,33)(17,31,45,35)(19,7,47,9);
Rubik := Group(pH,pB,pA,pP,pG,pD);
# Pocket=le groupe des permutations du Pocket (= Rubik sans arêtes)
#pH := (1,3,5,7)(17,21,25,29)(19,23,27,31) ;
#pB := (9,15,13,11)(33,45,41,37)(35,47,43,39);
#pA := (1,35,11,23)(17,9,37,3)(19,33,39,21);
#pP := (7,25,13,45)(29,27,41,47)(31,5,43 ,15);
#pG := (3,39,13,27)(21,11,41,5)(23,37,43,25);
#pD := (1,29,15,33)(17,31,45,35)(19,7,47,9);
#Pocket := Group(pH,pB,pA,pP,pG,pD);
# Tori=le groupe des permutations du Tori (Rubik sans sommets)
#pH := (2,4,6,8)(26,28,30,32);
#pB := (18,24,22,20)(42,48,46,44);
#pA := (2,34,18,36)(26,10,42,12);
#pP := (6,38,22,40)(30,14,46,16);
#pG := (4,12,20,14)(28,36,44,38);
#pD := (8,16,24,10)(32,40,48,34);
#Tori := Group(pH,pB,pA,pP,pG,pD);
#################
G := Rubik ;;
Gtxt := "Rubik" ;;
J := Iso ;;
Jtxt := "J" ;;
Jcjg := Sum(J,f -> Size(Centralizer(G,f))) / Size(J);;
Print("\n\n ",Gtxt," = ", Size(G), "\n" );
Print("\n classe ",Jtxt,"-cjg = ", Jcjg, "\n" );